Projectile Motion with (Quadratic) Drag
Posted on October 31, 2013
Projectile motion is discussed and worked out in nearly every college physics, calculus, and dynamics class, but examples always seem to neglect or over-simplify drag. In this post we will tackle an analytic solution that models drag for a falling object.
Let’s suppose we are dropping a ball from a height \(h_0\) with a velocity \(v_0\). In a vaccuum, the only force is gravity, $mg$. Then projectile motion without drag begins with Newton’s second law $$F_{net}=mg=ma \rightarrow a=g.$$ Acceleration can then be twice integrated with respect to time, yielding $$p(t)=\frac{g}{2}t^2+v_0t+h_0.$$ Given a constant force (i.e. not dependent on time or velocity) this is a simple integration with respect to time and the math is rather elementary. We can make it much more challenging by inserting an additional force term, drag, which is dependent on velocity: $$F=mg-D =ma \rightarrow a=g-D/m.$$ Many approximations for drag can be applied, but the most accurate model is $$D=1/2 \rho v^2\cdot c_d\cdot A.$$ Here \(c_d\) is coefficient of drag (dimensionless), A is the cross-sectional area, and \(\rho\) is the density of the medium the object is falling (e.g. air is $1.225 ~ \mathrm{kg}/\mathrm{m}^3$). Let’s jump into the math. $$a=g-D/m=g-\frac{\rho\cdot c_d\cdot A}{2m}v^2.$$ Now let \(a=dv/dt\) and for simplicity let \(k^2=\frac{\rho\cdot c_d\cdot A}{2mg}\). Coincidentally, $\frac{1}{k}$ is also the terminal velocity of a falling object. We have \begin{eqnarray} \frac{dv}{dt} &=& g-gk^2 v^2 \\ g\cdot dt &=& \frac{dv}{1-k^2 v^2}. \end{eqnarray} In its current form, this is not a simple integration. It can be evaluated with the hyperbolic arc-tangent, but to keep the equations in terms of more recognizable functions we will instead apply a partial fraction expansion $$\frac{dv}{1-k^2 v^2}=\frac{1}{2k}\left[\frac{dv}{v-1/k}-\frac{dv}{v+1/k}\right].$$
If this is confusing, you can review partial fraction expansions here
Now we can integrate \begin{eqnarray} g\cdot dt &=& \frac{1}{2k} \left[\frac{dv}{v+1/k}-\frac{dv}{v-1/k}\right]. \\ g\cdot t &=& \frac{1}{2k} \left[\ln(v+1/k)-\ln(v-1/k)\right]+C_1. \end{eqnarray}
We now have time as a function of velocity, but that isn’t very useful. Let’s see if we can solve for $v$: \begin{eqnarray} g\cdot t &=& \frac{1}{2k} \left[ \ln(v+1/k)-\ln(v-1/k) \right] +C_1 \\ g\cdot t &=& \frac{1}{2k}\cdot\ln\left[\frac{v+1/k}{v-1/k}\right]+C_1 \\ 2gk\cdot t+C_2 &=& \ln\left[\frac{v+1/k}{v-1/k}\right]\\ \end{eqnarray}
Now we can exponentiate both sides
\begin{eqnarray} Ce^{2gk\cdot t}=\frac{v+1/k}{v-1/k}=\frac{2/k}{v-1/k}+1. \\ \end{eqnarray} Now we can solve for $v$. \begin{eqnarray} v &=& \frac{2/k}{Ce^{2gk\cdot t}-1}+1/k. \\ &=& \frac{1}{k}\left(\frac{2}{Ce^{2gk\cdot t}-1}+1\right). \\ \end{eqnarray} Now we eliminate that pesky \(C\) by applying an initial condition for velocity. We are simply dropping something so let \(v(0)=0\).
We have \begin{eqnarray} v &=& \frac{1}{k}\left(\frac{2}{Ce^{2gk\cdot 0}-1}+1 \right) \\ &=& \frac{1}{k}\left(\frac{2}{C-1}+1 \right) \rightarrow C=-1. \end{eqnarray} Therefore $$v = \frac{1}{k}\left(1-\frac{2}{e^{2gk\cdot t}+1}\right).$$ Velocity is all fine and dandy, but what we are really after is position. This requires one more integration, but fortunately it’s a little simpler: This takes a little rewriting u-substitution. We have \begin{eqnarray} \frac{dp}{dt} &=& \frac{1}{k}\left(1-\frac{2}{e^{2gk\cdot t}+1}\right) \\ &=& \frac{1}{k}\left(1-\frac{2e^{2gk\cdot t}+2}{e^{2gk\cdot t}+1}+\frac{2e^{2gk\cdot t}}{e^{2gk\cdot t}+1}\right) \\ &=& \frac{1}{k}\left(1-2+\frac{2e^{2gk\cdot t}}{e^{2gk\cdot t}+1}\right). \end{eqnarray}
Now this is in a form where we can intuitively apply $u$-substitution. We have \begin{eqnarray} p=\frac{1}{gk^2}\ln[e^{2gk\cdot t}+1]-\frac{t}{k}+C. \end{eqnarray} Now if we apply the initial condition \(h(0)=h_0\) we have \begin{eqnarray} p &=& \frac{1}{gk^2} \ln\left[e^{2gk\cdot t}+1\right]-\frac{\ln(2)}{gk^2}-\frac{t}{k}+h_0. \\ &=& \frac{1}{gk^2} \ln\left[\frac{e^{2gk\cdot t}+1}{2}\right]-\frac{t}{k}+h_0. \end{eqnarray}
Let's put this to use with a quick example. Let's say we are dropping two balls off a tower $56~\mathrm{m}$ tower. They have the same cross-sectional area $A=1/3 ~ \mathrm{m}^2$ and drag coefficient $c_d=0.5$, but have different masses of $1 ~ \mathrm{kg}$ and $5 ~ \mathrm{kg}$. We can use the above formula to find how long it takes them to hit the ground.
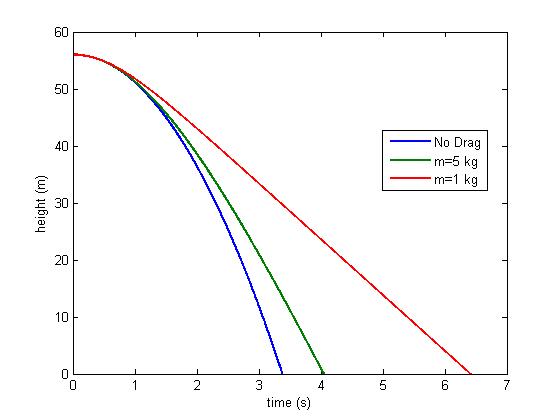
Clearly accounting for drag is important if the object falling is very light, very large, or is falling through a medium with a high density.