Probabilistic Availment
Posted on December 18, 2019
Introduction
This post will tackle two probability questions inspired by a recent Civil Procedure practice test I took. Consider a company that randomly buys $300$ loans from houses all over the United States. What is the probability that at least one of the loans is for a house in Florida? What is the probability that there is a loan for at least one house in each of the fifty states?
The legal purpose for this analysis is determining purposeful availment, a murky part of personal jurisdiction summarized (over)simply enough as "if you meant to business in a certain state, you can be sued there." If a business only had $50$ loans, then they could make a much better case that they don't intend to be subject to a particular state. But for a large number like $300$, intuition tells you that the likelihood is much higher.

Is Florida Targeted?
For the sake of simplicity, assume each state is targeted with equal probability. You could recast the problem as $300$ state quarters if it helps get over the hump of population difference between states like Wyoming and California.
If there was just one state, the probability that it isn't Florida is $\frac{49}{50}=.98$. Similarly, if $300$ states are selected, the probability none are Florida is just $.98^{300}$. So the probability that at least one is Florida is the complement:
$$ 1-.98^{300} = 99.8\%.$$With this many loans there is high certainty that Florida is at least one of them. Side note: $99\%$ may not be high enough, read the top of page 20 of Justice Kagan's dissent in the recent SCOTUS gerrymandering case. Apparently $99\%$ wasn't good enough for the majority.
So how many are loans are sufficient for $50\%$, $95\%$, or $99.7\%$ certainty? This is a simple exercise in logarithms. Let there be $n$ loans and a certainty $p$. Then
\begin{eqnarray*} 1-.98^n &=& p \\ .98^n &=& 1-p \\ \log(.98^n) &=& \log(1-p) \\ n\log(.98) &=& \log(1-p) \\ n &=& \frac{\log(1-p)}{\log(.98)} \\ \end{eqnarray*} So for $p=50\%$ you need $n=35$ houses, $p=95\%$ you need $n=149$ houses, and for $p=99.7\%$ you need $n=288$ houses.Is Every State Targeted?
This is a considerably harder problem. We must consider significantly more cases than just Florida's absence. First, we can tackle it with a simulation for some perspective. The following code does the trick.
import random
num_simulations = 10000
num_states = 50
num_loans = 300
count = 0
for _ in xrange(num_simulations):
coll = set([])
for _ in xrange(num_loans):
coll.add(random.randrange(num_states))
if len(coll) == 50:
count += 1
print count/float(num_simulations)
This is helpful, but not satisfying. Can we solve this analytically?
My first intuition was an extension of the previous section, just take the probability of one state and multiply it out 50 times, $\left(1-.98^{300}\right)^{50}$. Unfortunately, there is an oversight here. The discrepancy is hard to spot with $50$ states, but becomes more and more apparent as the problem is recasted with fewer states.
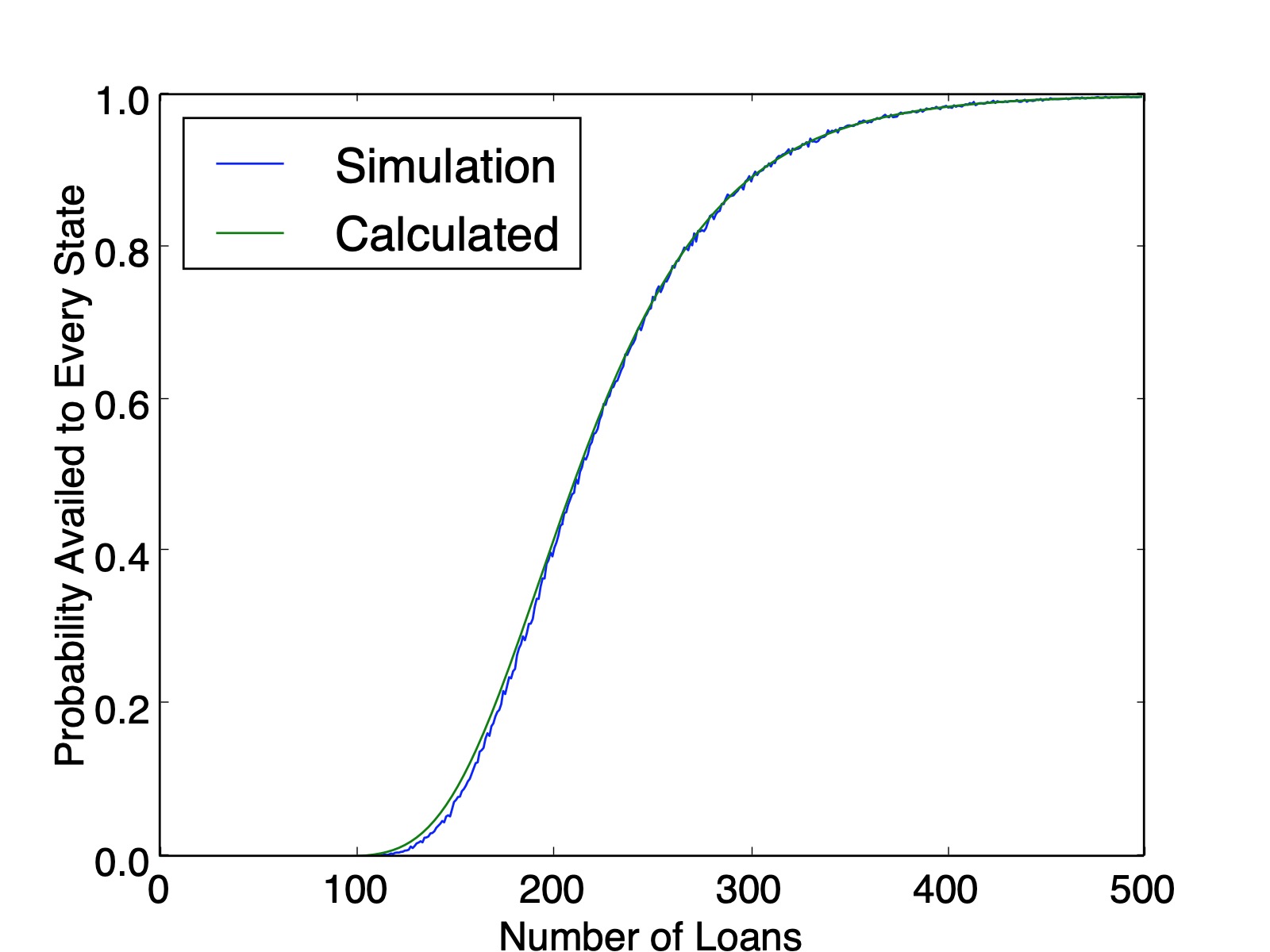
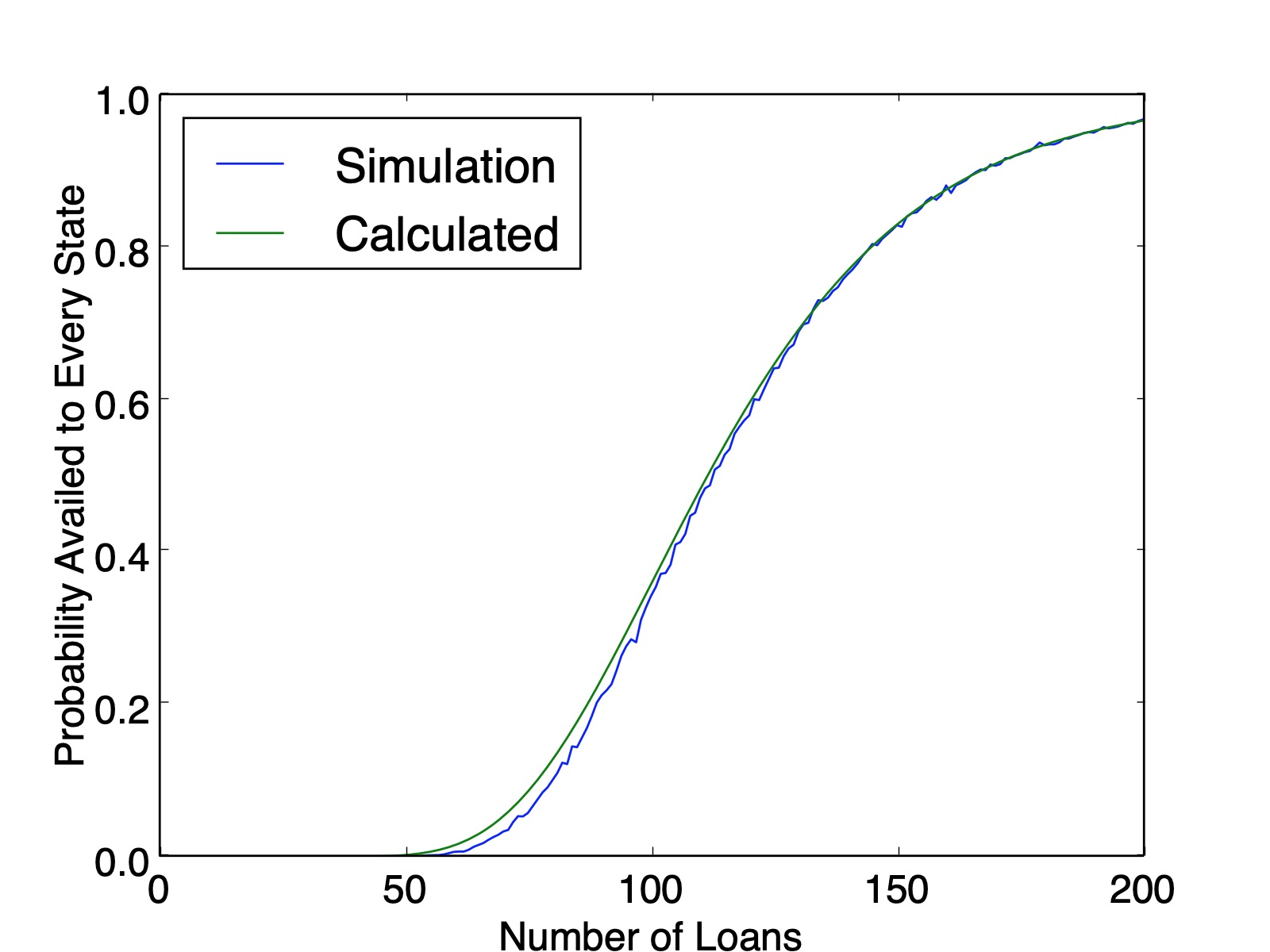
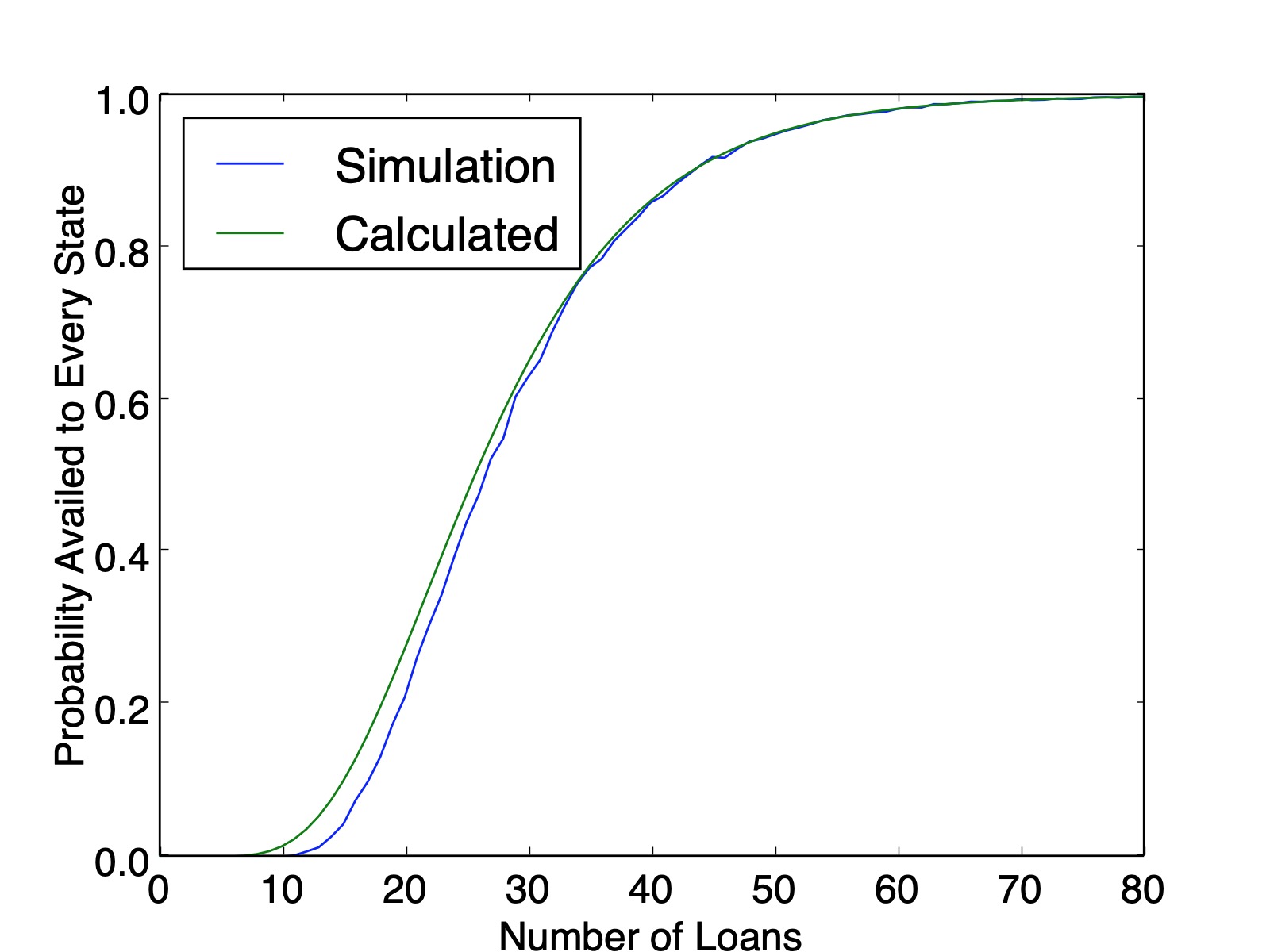
The issue here is that after you determine that Florida is present in the list and you try to move on to next state, that subsequent probability is constrained by how many times Florida came up in the first pass through the list. This dependence cascades down with combinatorial complexity.
Counting a Simpler Case
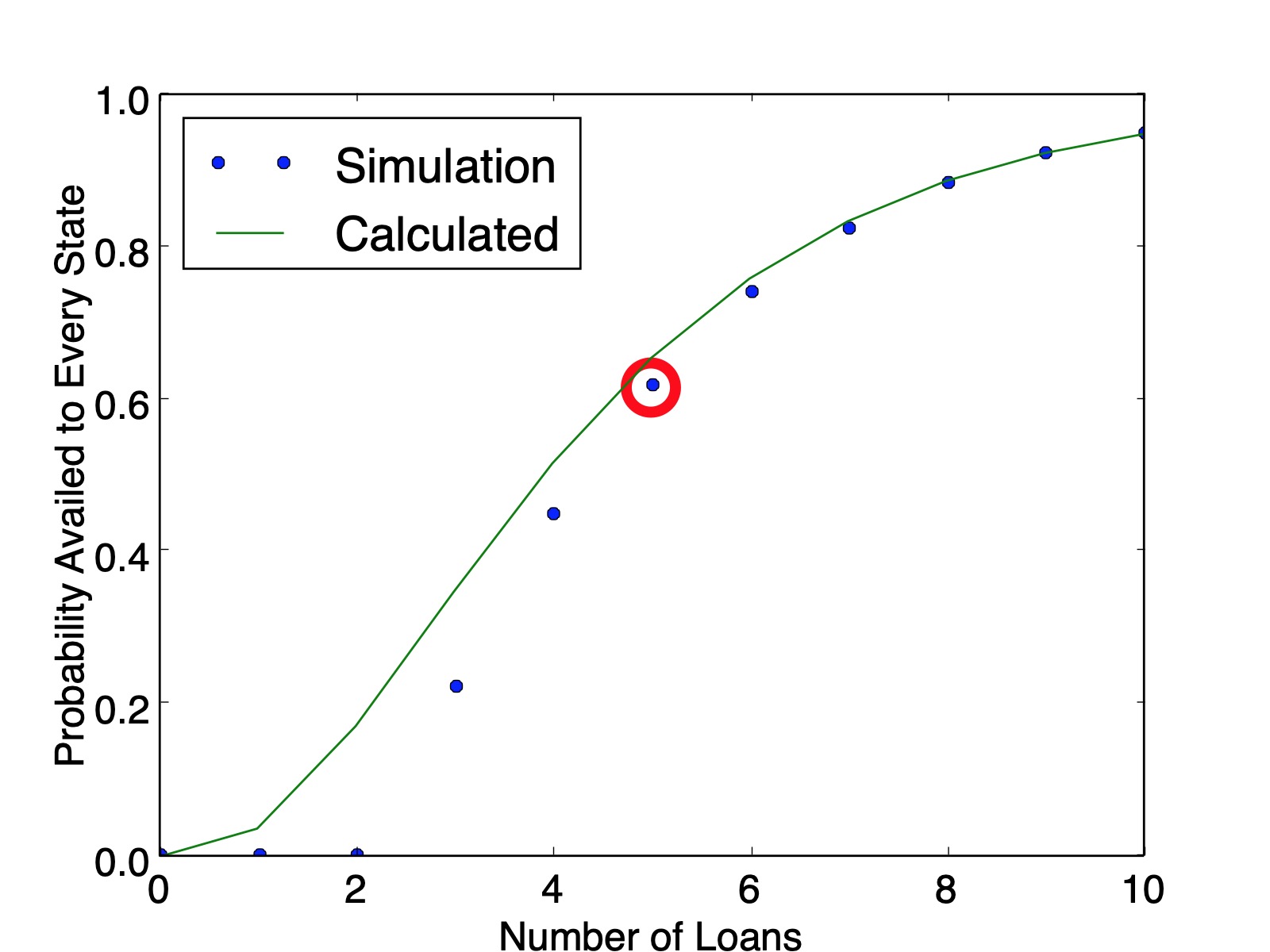
For illustrative purposes, let's walk through a simpler case, $3$ states and $5$ loans. This will "prove" the accuracy of the simulation and lay out the means for (and complexity of) an algorithm to tackle larger numbers.
There are $3^5=243$ possible ways for the loans to be divided up. We will brute force count all $243$ outcomes by arranging into three buckets: one state, two state, and three state. Call the states $A$, $B$, and $C$ and treat the loan distribution like 5-letter words comprised of these letters.
The one-state cases are (quite trivially) $AAAAA$, $BBBBB$, and $CCCCC$.
It gets trickier with more states. For a two-state solution, consider the alphabetical pairs $(A,B)$, $(A,C)$, and $(B,C)$. These pairs can fit into the words summarized in the table below. (The first letter in the ordered pair matches with $X$ and the second with $Y$.)
| Pattern | Number of Combinations |
|---|---|
| $XXXXY$ | $\binom{5}{1}=5$ |
| $XXXYY$ | $\binom{5}{2}=10$ |
| $XXYYY$ | $\binom{5}{3}=10$ |
| $XYYYY$ | $\binom{5}{4}=5$ |
Using the $3$ pairs and $5+10+10+5=30$ arrangements, there are $3\cdot 30=90$ two-state solutions. Ordering the three pairings above ensures we don't overcount. For a three-state solution, there is only one alphabetical order $(A,B,C)$. These pairs can fit into the words summarized in the table below.
| Pattern | Number of Combinations |
|---|---|
| $AAABC$ | $\frac{5!}{3!}=20$ |
| $AABBC$ | $\frac{5!}{2!2!}=30$ |
| $AABCC$ | $\frac{5!}{2!2!}=30$ |
| $ABCCC$ | $\frac{5!}{3!}=20$ |
| $ABBCC$ | $\frac{5!}{2!2!}=30$ |
| $ABBBC$ | $\frac{5!}{3!}=20$ |
So there are $150$ three-state solutions. Therefore, the probability that every state is availed is $\frac{150}{243}=0.6173$, which matches the simulation value plotted below ($0.6161$ calculated from $100,000$ simulations). And as a sanity check, our counting method produced $150+90+3=243$ lists.
Another Way to Count The Same Thing
Consider the following alternate approach for counting the $5$-loan, $3$-state problem. We will generate the number of lists where the states $A$, $B$, and $C$ show up $2$, $2$, and $1$ times respectively. First, state $A$ can show up in $\binom{5}{2}=10$ of the five locations. Remove the $2$ instances of state A from the list; now state $B$ can show up in $\binom{3}{2}=3$ remaining ways. Once $B$'s locations are picked, there is only one spot remaining for state $C$. Therefore the total number of ways to order this set is $\binom{5}{2}\cdot \binom{3}{2}\cdot \binom{1}{1} = 30$.
The same procedure is computed for all $\binom{4}{2}=6$ partitions of the $5$ states into $3$ non-empty groups in the table below.
| Pattern | Number of Combinations |
|---|---|
| $(1,1,3)$ | $\binom{5}{1}\cdot \binom{4}{1}\cdot \binom{3}{3}=20$ |
| $(1,2,2)$ | $\binom{5}{1}\cdot \binom{4}{2}\cdot \binom{2}{2}=30$ |
| $(1,3,1)$ | $\binom{5}{1}\cdot \binom{4}{1}\cdot \binom{1}{1}=20$ |
| $(2,1,2)$ | $\binom{5}{2}\cdot \binom{3}{1}\cdot \binom{2}{2}=30$ |
| $(2,2,1)$ | $\binom{5}{2}\cdot \binom{3}{2}\cdot \binom{1}{1}=30$ |
| $(3,1,1)$ | $\binom{5}{3}\cdot \binom{2}{1}\cdot \binom{1}{1}=20$ |
This approach affords us a new insight: a clear look at the combinatorial complexity required to count this. We must count the ways to arrange letters for every partition of loans among states. For $5$ loans and $3$ states there are $\binom{4}{2}=6$ partitions, but for $300$ loans and $50$ states there are $\binom{299}{49}=5.19\times 10^{56}$ partitions.
It also affords a nice way to visualize different computations. The $5$-loan, $3$-state problem is a bit bland, but here is a flow chart of the paths to calculate all arrangements for the $6$-loan, $4$-state problem.
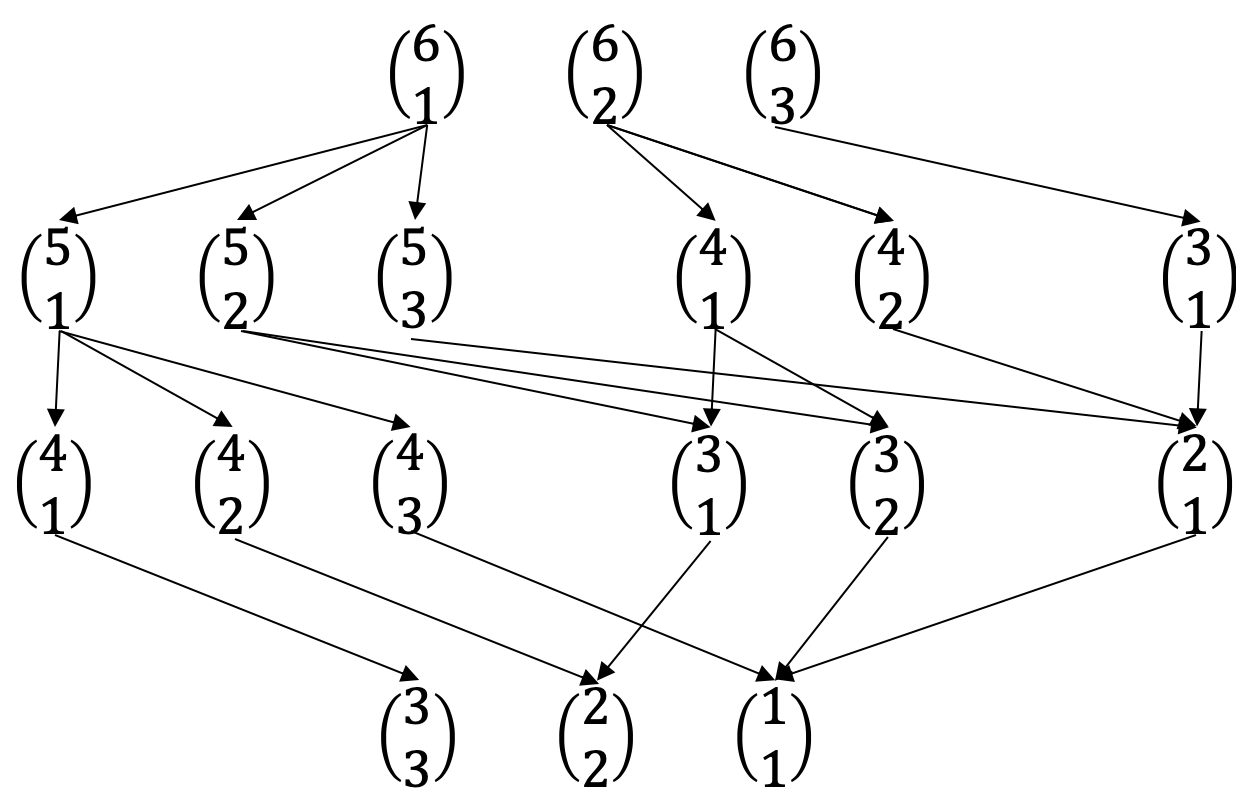
The recursive nature of these patterns lends itself to either recursive solutions, or potentially even a dynamic programming algorithm. That said, the simulations were a lot easier to generate and the combinatorial complexity of the problem makes it intractable for large numbers.
Manipulating Res Ipsa
Posted on October 13, 2019
Introduction and Example
A recent torts cases from class (Byrne v. Boadle) served as the introduction to a class of problems where negligence could be considered probabilistically. This set of problems mirrors the more well-known "false positive" problem. Here are two ways to state what is mathematically the same exercise.
"False Positive" problem: A disease afflicts $0.1\%$ of a population. A test exists for the disease, and will show positive $90 \% $ of the time if you have the disease and $1\%$ of the time if you don't (false positive). If you test positive, what is the probability you have the disease?
Negligence problem: Employees of a company act negligently $0.1\%$ of the time they load barrels next to a window. If they act negligently, an accident occurs $90\%$ of the time. When they are not negligent, an accident occurs $1\%$ of the time. If an accident occurs, what is the probability it was due to negligence?
Both have the same solution (we'll use the negligence nomenclature). Define $P_1$, $P_2$, and $P_3$ per the table below.
| Probability | Disease Problem | Negligence Problem |
|---|---|---|
| $P_1=1\%$ | False positive | Accident, not acting negligently |
| $P_2=90\%$ | True positive | Accident, acting negligently |
| $P_3=0.1\%$ | Prevalence of disease | Rate of negligence |
Let's say an accident occurred. The probability an accident occurs through negligence is $P_{negligence}=P_2\cdot P_3=0.00999$. The probability an accident occurs without negligence is $P_{no-negligence}=P_1\cdot(1-P_3) = 0.0009$. Therefore the probability it was due to negligence is: $$ \frac{P_{negligence}}{P_{negligence}+P_{no-negligence}} = 8.3\%.$$ So $8.3\%$ of the time it is due to negligence (or isomorphically, there is an $8.3 \% $ chance you have the disease despite a positive test).
So should this example drive our intuition? Unless this pattern of low rates of negligence holds for a majority of inputs, the answer is a resounding no.
Let's change the problem slightly by making the probability of accident from non-negligence $P_1=0.1\%$ and the rate of negligence $P_3=1\%$. Intuition would tell you negligence is more likely to have been the cause, but by how much? If you work through the same math, the probability the accident was due to negligence now becomes $90.1\%$. Clearly, this problem is susceptible to manipulation through small changes in the inputs.
DIY Inputs
Try a few different cases yourself and see if you can game the outcome. What are the driving variables?Changing $P_1$ and $P_3$
We were able to "flip" the outcome by flipping $P_1$ and $P_3$, so let's look at the probability of negligence as we vary those two variables. Plots can be generated with the following code.
import matplotlib.pyplot as plt
steps = 201
array2d = [range(steps) for _ in range(steps)]
interval = .0005
for i in range(steps):
for j in range(steps):
p1 = interval*(i+1) # probability of drop if properly handled
p2 = .20 # probability of drop if improperly handled
p3 = 1-interval*(j+1) # probability of handled properly
pa = p1*p3 # handled properly but dropped
pb = (1-p3)*p2 # handled improperly and dropped
p_proper = pa/(pa+pb)
array2d[j][i] = p_proper
plt.contourf(array2d, 9, vmin=0.0, vmax=1.0, origin='lower',
extent=[interval * 100, interval * steps * 100, interval * 100, interval * steps * 100],
cmap='seismic')
cbar=plt.colorbar()
plt.xlabel('$P_1$, probability of accident, not acting negligently (%)')
plt.ylabel('$P_3$, rate of negligence (%)')
plt.title('Probability that Accident Happened through Negligence, $P_2 = 20\%$')
cbar.set_ticks([0, .2, .4, .6, .8, 1])
cbar.set_ticklabels([0, .2, .4, .6, .8, 1])
plt.show()
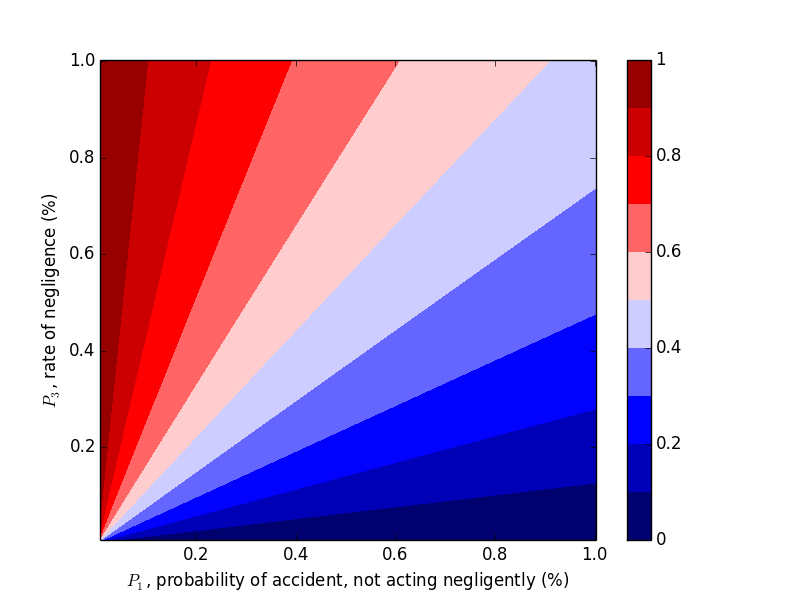
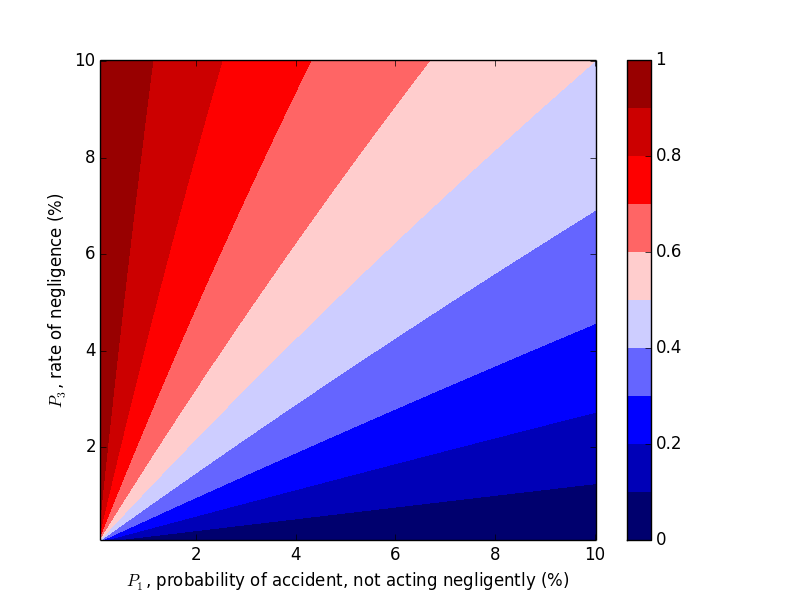
This trend makes sense in hindsight, but one should hardly be expected to carry this intuition around with them, naturally or otherwise.
Changing $P_2$
Now let's work with $P_2$. Compare the above plots where $P_2=0.9$ to the plots below where $P_2=0.2, 0.5$. We would expect decreasing $P_2$, probability of an accident given negligence, to decrease the probability of negligence given an accident, which the plots below confirm.
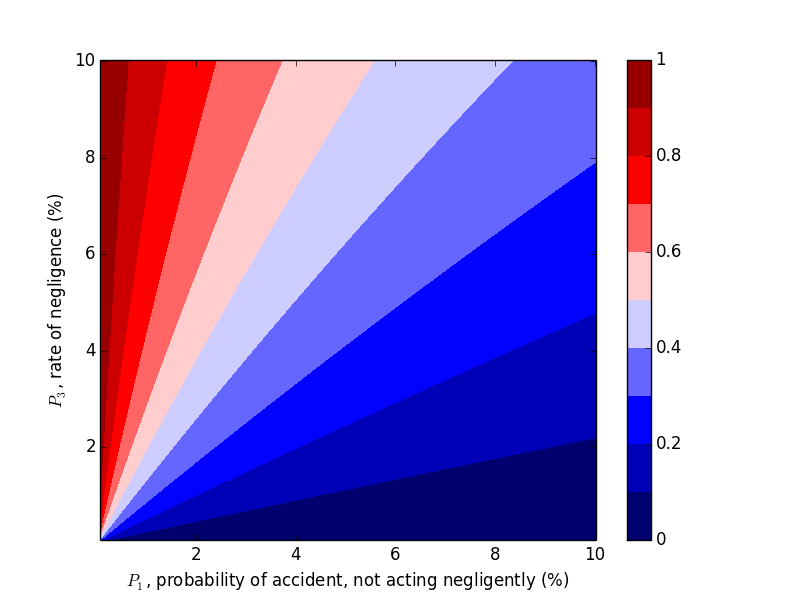
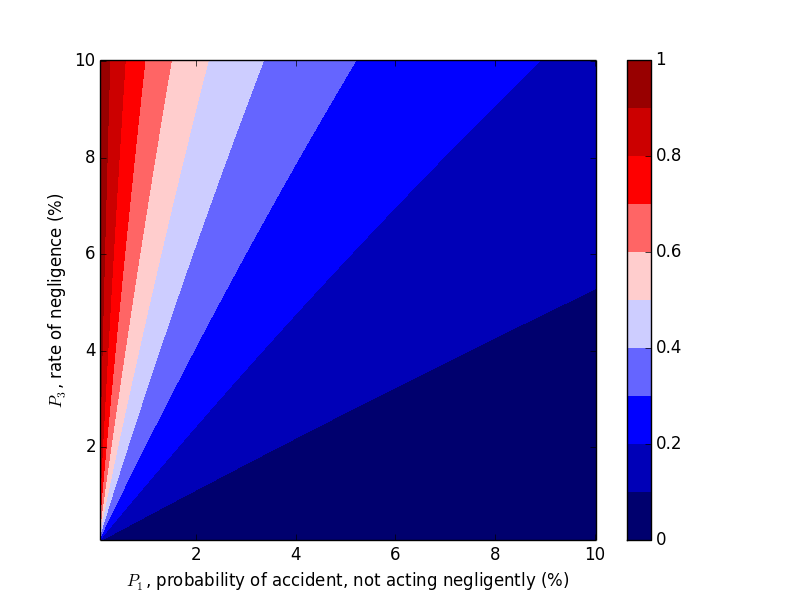
Takeaways
With these results, we can develop a general intuition:
- If $P_2$ is sufficiently low, an accident is probably not due to negligence.
- If $P_2$ is sufficiently high and $P_1>P_3$, then the accident was probably not due to negligence.
- If $P_2$ is sufficiently high and $P_1 < P_3$, then the accident was probably due to negligence.
That said, a more important takeaway here is simpler: don't let a limited data set drive your intuition. Look at the sensitivity of the variables involved, and look at a wide swath of results before jumping to conclusions. And unless you have a clear reason to, don't arbitrarily assume probabilities. You probably don't know the difference between $0.1 \%$ and $1 \%$ without a good data set to aid you.
Optimal HORSE Strategy
Posted on July 14, 2019
Below is a solution to the Classic problem posed on July 12's edition of the Riddler on fivethirtyeight.com, "What’s The Optimal Way To Play HORSE?".
We will first introduce the game, then walk through a simulation, then the analytic solutions for the simplified game of $\mathrm{H}$ then the full game of $\mathrm{HORSE}$. We'll show that the optimal strategy regardless of the number of letters in the game is to always shoot the highest percentage shot (short of a 100% shot).
Intuitive Strategies
Two strategies immediately come mind. First, take a shot that maximizes the probability of you making a basket and him missing.
The second, and provably better strategy is to take advantage of the one thing you have (you are equally good shooters). You get to go first, so take full advantage of that turn, and maximize the probability of scoring a point before you miss.
Intuitive strategies are meaningless unless testing, so let's see what works best.
Simulation and Optimal Strategy
The code below is a bare bones implementation of a simulation. Player A and Player B can be assigned two different strategies, a_prob and b_prob, and the length of the game can be changed.
import random
def make_basket(prob):
if prob > random.random():
return True
else:
return False
def run_simulation(a_prob, b_prob, horse):
a_score = 0
b_score = 0
a_turn = True
while True:
if a_turn:
if make_basket(a_prob):
if make_basket(a_prob):
pass # both make
else:
a_score += 1 # a make, b miss
else:
a_turn = False # a misses, it's b's turn
else:
if make_basket(b_prob):
if make_basket(b_prob):
pass # both make
else:
b_score += 1 # b make, a miss
else:
a_turn = True # b misses, it's a's turn
if a_score >= horse or b_score >= horse:
break
return a_score, b_score
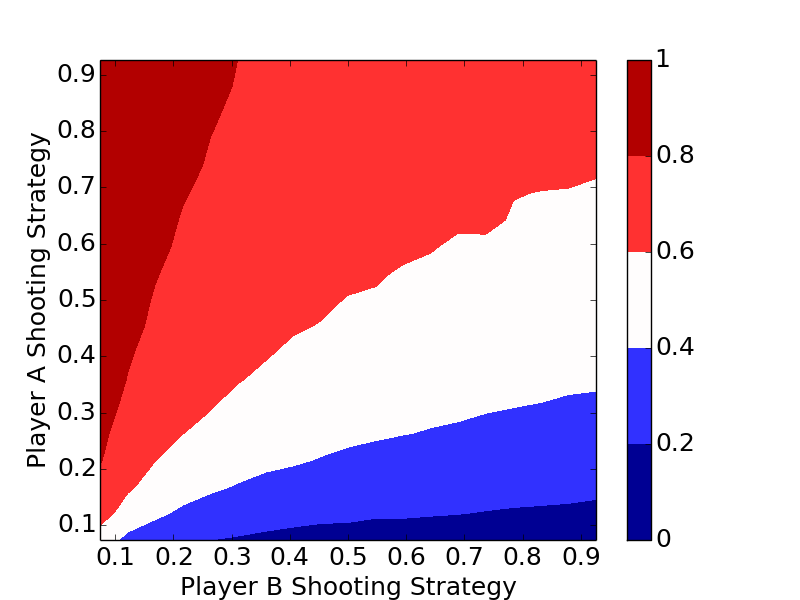
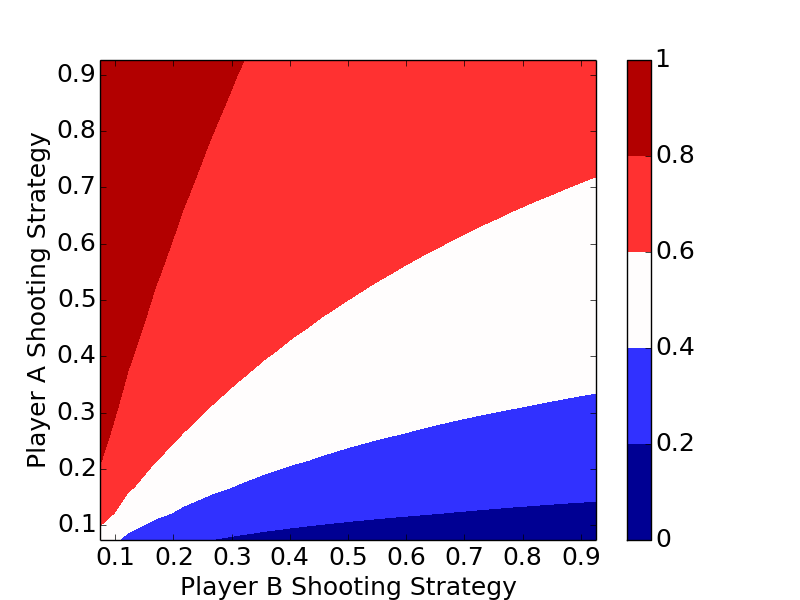
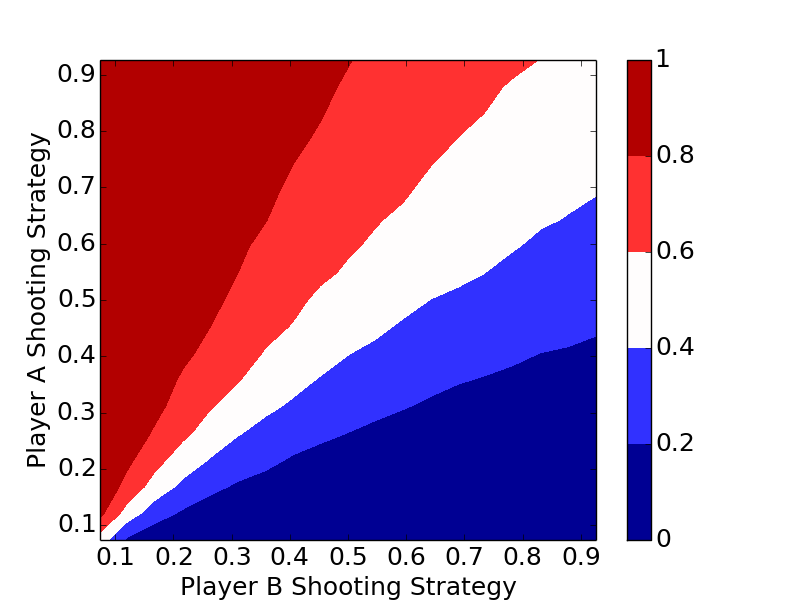
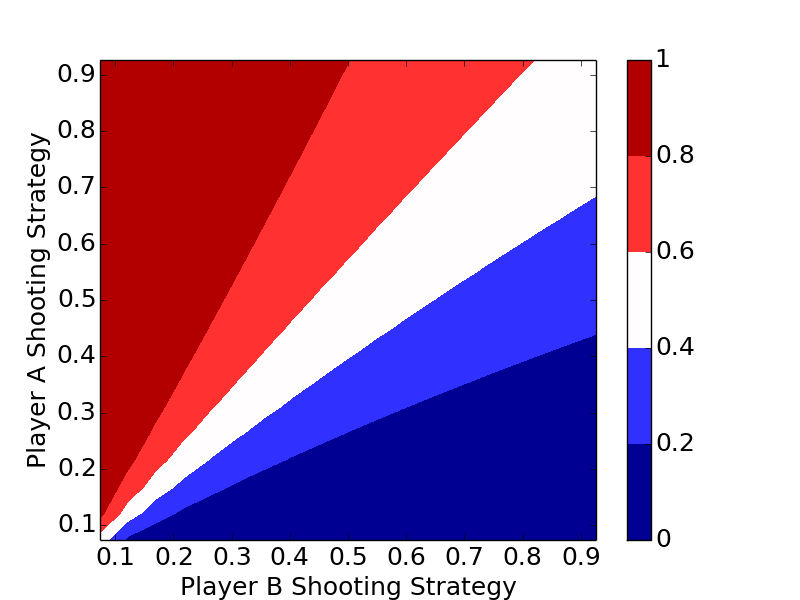
The plots clearly show the optimal strategy regardless of the number of letters in the game is to always shoot the highest percentage shot (short of a 100% shot).
Analytic Solution to $\mathrm{H}$
Let's consider the probability of Player A winning a point before losing their turn. Let $a$ be the probability of Player A making a basket. Then they could make a point in two shots with $p_2(a)=a(1-a)$, in four shots with $p_4(a)=a^3(1-a)$, or in general, in $2n$ shots with $p_{2n}(a)=a^{2n-1}(1-a)$. Therefore, the probability $p_A$ of winning a letter before losing their turn is $$p_A=\sum{p_i(a)}=a(1-a)+a^3(1-a)+... = \frac{a(1-a)}{1-a^2}=\frac{a}{a+1}.$$
The maximum value of this function on $[0,1]$ occurs at $a=1$, with $p_A(a)=0.5$. We wouldn't want to shoot a basket neither player ever misses, a trivial solution and never ending game, but we want to pick the shot closest to that.
We'll expand from winning a point without losing a turn, to winning the game of $H$, another geometric sequence. Let the player's probabilities of winning a point without losing a turn be $p_A$ and $p_B$ respectively. Player A could win on the first turn with probability $p_{AH_{1}}=p_A$, on the third turn with probability $p_{AH_{3}}=(1-p_A)(1-p_B)p_A$, and in $2n+1$ turns with probability $$p_{AH_{ 2n+1}}=(1-p_A)^{n}(1-p_B)^np_A$$
Similarly, the probability that Player A wins $H$, $p_{AH}$, is this sum $$p_{AH}=\sum{p_{AH_{2n+1}}}= \frac{p_A}{1-r}.$$ Where $p_A=\displaystyle\frac{a}{a+1}$, $p_B=\displaystyle\frac{b}{b+1}$, and $r=(1-p_A)(1-p_B)$.
As a sanity check, one could sum the terms of the geometric series for the probability of Player B winning, $\displaystyle\frac{(1-p_A)p_B}{1-r}$, add it to the probability of A winning, and find their sum is one, as it should be.
Analytic Solution to $\mathrm{HORSE}$
Expanding to multi-letter games is no longer a game of compounded geometric series, but instead of counting combinations. You can start by thinking of winning $\mathrm{HORSE}$ the same way as winning a five-game series. Unfortunately, it gets a little more complicated; your probability of winning a letter is based off whether or not you won the previous letter.
Let $A$ denote a Player A point win, and $B$ denote a Player B point win. Consider the game $AAAAA$. On each round, Player A starts, so they have the advantage; their probability of winning each point is $P_{AH}$.
Now consider, $ABAAAA$. The Player A win on point 3 following the Player B win, has the lower likelihood $(1-P_{BH})$ of occurring since Player B had the advantage of starting with the ball after winning point 2.
What makes the counting challenging is that the sequences $AABBBAAA$ and $ABABABAA$, for example, do not have the same probabilities for Player A winning. The first only has two "switches" from who is in control (shooting first), where the second has six switches, changing the probabilities in different ways. There is no way around working through each of the individual $1+5+15+35+70=126$ cases for Player A winning in five through nine games respectively.
The code below summarizes this counting.
probs = [.05*i for i in range(1,20)]
for a in probs:
for b in probs:
pa = a / (1 + a)
pb = b / (1 + b)
r = (1 - pa) * (1 - pb)
pAH = pa / (1 - r) # probability a wins going first
pBH = pb / (1 - r) # probability b wins going first
pAB = (1 - pAH, pAH)
cum_p = 0 # cumulative probability
for s in ['1111', '01111', '001111', '0001111', '00001111']:
tups = list(perm_unique(s))
for tup in tups:
seq = [int(i) for i in list(tup)+['1']]
p = pAB[seq[0]]
for i in range(1, len(seq)):
if seq[i-1] == 0 and seq[i] == 0:
p *= pBH
elif seq[i-1] == 1 and seq[i] == 0:
p *= (1 - pAH)
elif seq[i-1] == 0 and seq[i] == 1:
p *= (1 - pBH)
elif seq[i-1] == 1 and seq[i] == 1:
p *= pAH
cum_p += p
print cum_p,
print ""
My code makes use of some StackOverflow code to make unique permutations.
Winning Lotería and Countdown
Posted on June 2, 2019
Updated on June 4, 2019
I made a few changes from the original post. I misread allowable order of operations (the equivalent of "parentheses are ok", which drastically increases solvable numbers). I decided to leave it in as an interesting twist on the problem.
I also left out the case of six small numbers (another misread), which I have since added.
Below are solutions to the Classic and Express problems posed on May 31's edition of the Riddler on fivethirtyeight.com, "Can You Win The Lotería?".
Riddler Express - Lotería
First, a brief solution to the Riddler Express. The question posed is: for $N=54$ total images, and $n=16$ images per player card, how often will the game end with one empty card of images?
Two things must be considered: how often do the two players have unique cards (a necessary condition), and if that is met, how often will an entire card be filled before any images on the second card are filled?
We must first consider the necessary condition that the players have unique images on their cards. It helps to think about image "selection" successively. The first player can pick their entire card without concern. Then the second player "picks" their images for the second card one by one. For $N=54$ and $n=16$, there are $54$ options, $54-16=38$ of which are favorable, so probability the first image for the second card is not on the first card is $\frac{38}{54}$. The second image cannot be the first (and will not be the previous image), so there are now $53$ options, $37$ of which are favorable, yielding a probability of $\frac{37}{53}$. Continuing this logic, the probability the cards are unique is
$$ \frac{38}{54}\cdot\frac{37}{53}\cdot\frac{36}{52}\cdot...\cdot\frac{23}{39} \approx 0.001054.$$In general, the probability can be written as
$$ \displaystyle\frac{\binom{N-n}{n}}{\binom{N}{n}}.$$ Second, assuming the two cards are unique, how often will you win before the other player crosses a single image off their card? The extraneous cards are meaningless, akin to burn cards. WLOG, if you have images $1$-$16$, your opponent has $17$-$32$, then the favorable outcomes are all $16!$ arrangements of your cards, followed by all $16!$ arrangements of your opponents outcomes. The total number of arrangements is $32!$, the arrangements of all cards. The probability is then $$ \displaystyle\frac{16!\cdot 16!}{32!} \approx 1.664\times 10^{-9}. $$In general, the probability can be written as
$$ \displaystyle\frac{(n!)^2}{(2n)!}. $$Note, there is no $N$ term in this expression. The simulation in the code below considers all $N$ cards to verify its invariance.
from ncr import ncr #n choose r
import numpy as np
def you_win(photo_order, n):
"""WLOG you have photos 0 to n-1, opponent has n to 2n-1
Check if all of your photos appear before any of your opponents"""
n_count = 0
for i in photo_order:
if i < n:
n_count += 1
if n <= i < 2*n:
return False
if n_count == n:
return True
def main():
N = 54 # Total number of photos
n = 16 # Number of photos per player
num_sim = 10000 # Number of simulations
# Simulate Unique
count = 0
for _ in xrange(num_sim):
list_1 = np.random.choice(N, n, replace=False) # Your photos
list_2 = np.random.choice(N, n, replace=False) # Opponent's photos
if set(list_1) & set(list_2): # Check for intersection
count += 1
print "probability unique:", \
ncr(N-n, n) / float(ncr(N, n)), \
1.0 - count / float(num_sim)
# Simulate You Win
count = 0
for _ in xrange(num_sim):
photo_order = np.arange(N)
np.random.shuffle(photo_order)
if you_win(photo_order, n):
count += 1
print "probability you win:", 1./ncr(2 * n, n), count / float(num_sim)
if __name__ == "__main__":
main()
Riddler Classic - Countdown
$\newcommand{\Lone}{\mathrm{L}_{1}}$ $\newcommand{\Ltwo}{\mathrm{L}_{2}}$ $\newcommand{\Lthree}{\mathrm{L}_{3}}$ $\newcommand{\Lfour}{\mathrm{L}_{4}}$ $\newcommand{\a}{\mathrm{a}}$ $\newcommand{\b}{\mathrm{b}}$ $\newcommand{\c}{\mathrm{c}}$ $\newcommand{\d}{\mathrm{d}}$ $\newcommand{\e}{\mathrm{e}}$The remainder of this post will focus on the countdown problem, namely a brute force approach to counting all possible outcomes in a reasonable amount of time, follwed by a discussion of results. See code here.
The most fruitful combination is shown to be $5$, $6$, $8$, $9$, $75$, $100$, which yields $691$ different three-digit numbers. The least fruitful is shown to be $1$, $1$, $2$, $2$, $3$, $25$, which yields only $20$ different three-digit numbers.
Statistics for the various strategies (selecting 1 through 4 large numbers) are summarized, and it is shown that selecting two large numbers is the most advantageous, followed closely by selecting three large numbers.
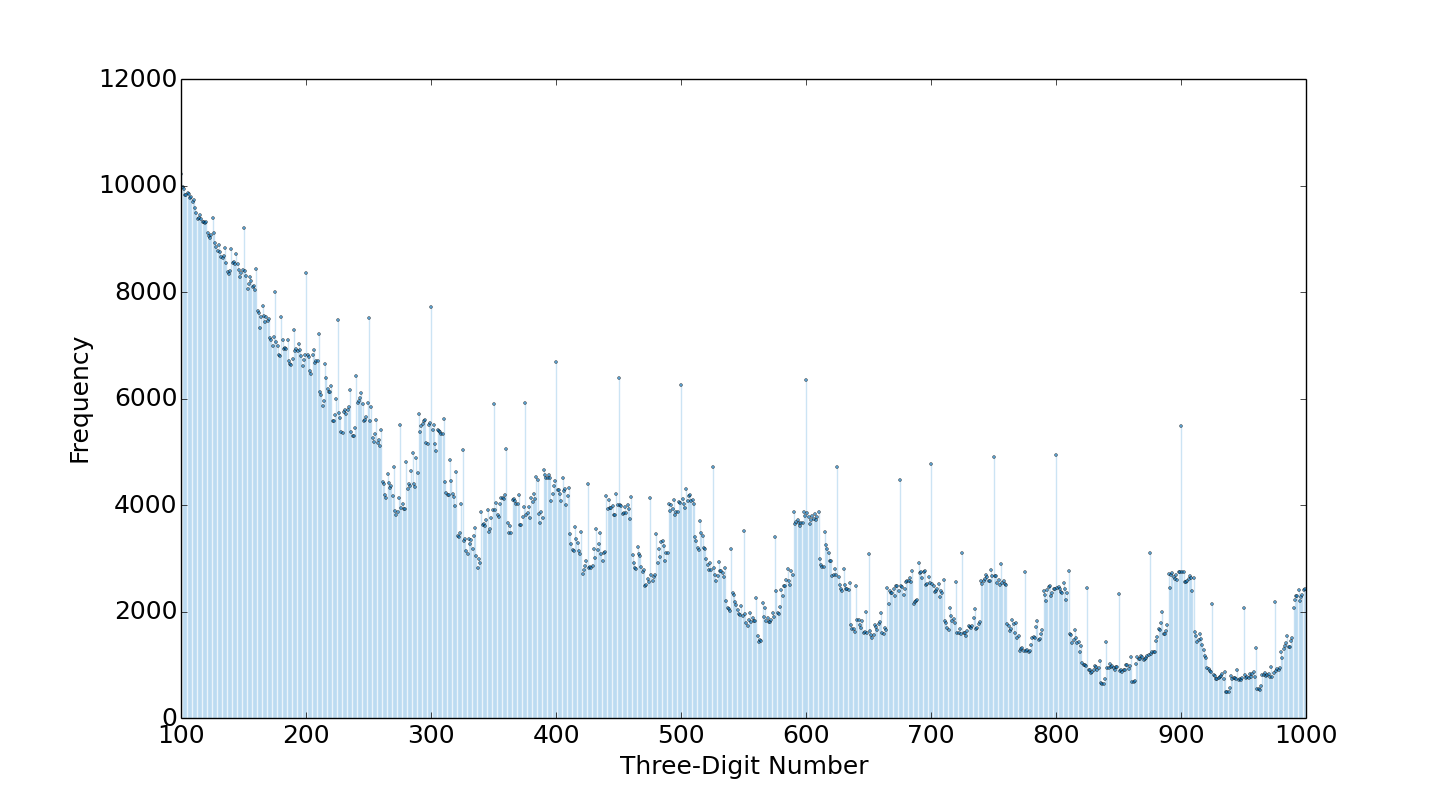
Finally, a histogram of the three-digit numbers frequency among the $10,603$ combinations shows what is intuitive, at least in hindsight: smaller three-digit numbers, and multiples of $25$, $50$, and especially $100$ are the most common.
Generating Combinations
First we must consider all possible combinations of the small and large numbers. We will denote large numbers with $\Lone$, $\Ltwo$, $\Lthree$, and $\Lfour$ and small numbers with $\a$, $\b$, $\c$, $\d$ and $\e$. A player can selected between zero and four large numbers, and the small numbers may repeat once. There are $11$ possible scenarios, divided by double lines in the table below by strategy.
| Pattern | Number of Combinations |
|---|---|
| $\a\b\c\d\e\mathrm{f}$ | $\binom{10}{6}$ |
| $\Lone\a\a\b\b\c$ | $\binom{4}{1}\cdot\binom{10}{2}\cdot\binom{8}{1}$ |
| $\Lone\a\a\b\c\d$ | $\binom{4}{1}\cdot\binom{10}{1}\cdot\binom{9}{3}$ |
| $\Lone\a\b\c\d\e$ | $\binom{4}{1}\cdot\binom{10}{5}$ |
| $\Lone\Ltwo\a\a\b\b$ | $\binom{4}{2}\cdot\binom{10}{2}$ |
| $\Lone\Ltwo\a\a\b\c$ | $\binom{4}{2}\cdot\binom{10}{2}\cdot\binom{8}{1}$ |
| $\Lone\Ltwo\a\b\c\d$ | $\binom{4}{2}\cdot\binom{10}{4}$ |
| $\Lone\Ltwo\Lthree\a\a\b$ | $\binom{4}{3}\cdot \binom{10}{1}\cdot \binom{9}{1}$ |
| $\Lone\Ltwo\Lthree\a\b\c$ | $\binom{4}{3}\cdot\binom{10}{3}$ |
| $\Lone\Ltwo\Lthree\Lfour\a\a$ | $\binom{4}{4}\cdot\binom{10}{1}$ |
| $\Lone\Ltwo\Lthree\Lfour\a\b$ | $\binom{4}{4}\cdot\binom{10}{2}$ |
Generating Permutations
These can be generated individually with the help of the Python itertools library. As a sample, consider $\Lone\Ltwo\a\a\b\c$.
import itertools
L_array = [25., 50., 75., 100.]
s_array = [float(i) for i in range(1, 11)]
for s in itertools.combinations(s_array, 3):
for L in itertools.combinations(L_array, 2):
for s0 in s:
loop_array = itertools.permutations(list(L) + list(s) + [s0])
This is probably the most complicated of the $11$ examples. Note the use of itertools.combinations vs itertools.permutations, the latter provides all arrangements and the former does not, which helps us reduce over counting. Over counting is not completely avoided however. The itertools library does not know that our two $\a$ values are repeats so we are over counting by a factor of $2$. This is not ideal, but the storage mechanism used (based on Python sets and dicts) eliminates error duplicate counting, so the only sacrifice is run time.
Considering Operators: $+-\times\div$
We will now take each permutation generated and loop through it's components left to right (i.e. consider the first number, then the first two numbers, then the first three, etc.). For example, given the permutation $100$, $50$, $10$, $2$, $7$, $4$, the first number "generated" is $100$. We then need to check all operations with the first two terms, $100+50$, $100-50$, $100\times 50$, and $100\div 50$ which yields $150$, another hit, but three numbers, $50$, $5000$, and $2$ that are not hits. Those last three numbers are not hits, but cannot be ignored since additional terms may turn them into hits; for example $100\times 50\div 10\div 2=250$ is another hit.
Challenges also arise with the implementation of addition, subtraction, multiplication and division operations in this left-to-right paradigm. We have $5$ spaces in between the $6$ numbers for each operation, for $4^5=1024$ possible permutations of the operators. However, we must only consider those where left to right operation satisfies order of operations. For example, $+$ $-$ $+$ $-$ $-$, $\div$ $\times$ $\div$ $\times$ $\div$, and $\times$ $\div$ $-$ $-$ $+$ are all acceptable but $+$ $\times$ $-$ $-$ $-$ because placing addition before multiplication is the equivalent of adding parentheses. Using the above example, $100+50+10\times2$
Acceptable orders of operation can be found with the following code. This finds all lists of five operators where all multiplication and division occur before all addition and subtraction.
operator_list = [] # Indices for operators, 0,1,2,3 is *,/,+,-
for i4 in xrange(4 ** 5):
cl = [i4 // 256 % 4, i4 // 64 % 4, i4 // 16 % 4, i4 // 4 % 4, i4 % 4]
if good_order(cl):
operator_list.append(cl)
print len(operator_list) # 192
Proving that this covers every possible case is not simple, but it makes intuitive sense that when all permutations of the 6 numbers are considered, the $192$ operators considered are exhaustive.
We now have everything we need to search for every combination. Full implementation can be found here.
A Brief Summary of Results
The combination $5$, $6$, $8$, $9$, $75$, $100$, yields $691$ different possible three-digit numbers, the most for any combination. The combination $1$, $1$, $2$, $2$, $3$, $25$, yields only $20$ possible combinations, the fewest. The top and bottom ten combinations are summarized in the tables below.
| Number | Number of three-digit numbers created |
|---|---|
| $5$, $6$, $8$, $9$, $75$, $100$ | $691$ |
| $5$, $7$, $8$, $9$, $75$, $100$ | $652$ |
| $6$, $7$, $9$, $10$, $75$, $100$ | $650$ |
| $6$, $8$, $9$, $10$, $75$, $100$ | $648$ |
| $3$, $8$, $9$, $10$, $75$, $100$ | $648$ |
| $2$, $5$, $6$, $9$, $75$, $100$ | $643$ |
| $5$, $6$, $8$, $9$, $50$, $100$ | $641$ |
| $5$, $6$, $7$, $9$, $75$, $100$ | $640$ |
| $2$, $5$, $8$, $9$, $75$, $100$ | $638$ |
| $4$, $7$, $9$, $10$, $75$, $100$ | $636$ |
| Number | Number of three-digit numbers created |
|---|---|
| $1$, $1$, $2$, $2$, $3$, $25$ | $20$ |
| $1$, $1$, $2$, $2$, $4$, $25$ | $21$ |
| $1$, $1$, $2$, $3$, $3$, $25$ | $25$ |
| $1$, $1$, $3$, $4$, $4$, $25$ | $34$ |
| $1$, $1$, $2$, $2$, $6$, $25$ | $35$ |
| $1$, $1$, $2$, $2$, $9$, $25$ | $35$ |
| $1$, $1$, $2$, $2$, $5$, $25$ | $35$ |
| $1$, $1$, $2$, $2$, $7$, $25$ | $35$ |
| $1$, $1$, $2$, $2$, $4$, $50$ | $36$ |
| $1$, $1$, $2$, $4$, $4$, $25$ | $36$ |
The table below shows that the best choice to pick two large numbers and four small numbers, but the strategy of picking three large is a close second. An outcome is defined as a three-digit number generated by a particular combination.
| Pattern | Arrangements | Total Outcomes | Average # of Outcomes |
|---|---|---|---|
| $\a\b\c\d\e\mathrm{f}$ | $210$ | $46,663$ | $222.2$ |
| $\Lone\a\a\b\b\c$ | $1440$ | $257,167$ | $178.6$ |
| $\Lone\a\a\b\c\d$ | $3360$ | $865,253$ | $257.5$ |
| $\Lone\a\b\c\d\e$ | $1008$ | $349,921$ | $347.1$ |
| One large | $253.5$ | ||
| $\Lone\Ltwo\a\a\b\b$ | $270$ | $58,221$ | $215.6$ |
| $\Lone\Ltwo\a\a\b\c$ | $2160$ | $694,966$ | $321.7$ |
| $\Lone\Ltwo\a\b\c\d$ | $1260$ | $574,520$ | $456.0$ |
| Two large | $\pmb{359.8}$ | ||
| $\Lone\Ltwo\Lthree\a\a\b$ | $360$ | $100,324$ | $278.7$ |
| $\Lone\Ltwo\Lthree\a\b\c$ | $480$ | $199,349$ | $415.3$ |
| Three large | $356.8$ | ||
| $\Lone\Ltwo\Lthree\Lfour\a\a$ | $10$ | $1,541$ | $154.1$ |
| $\Lone\Ltwo\Lthree\Lfour\a\b$ | $45$ | $10,619$ | $236.0$ |
| Four large | $221.1$ |
The histogram shows what we would intuitively expect, smaller numbers can be computed more often. There are also peaks at multiples of $25$, $50$, and especially $100$, another intuitive byproduct.
Flipping Astronauts
Posted on May 26, 2019
Introduction
This is a solution to the problem posed on May 24's edition of the Riddler Classic on fivethirtyeight.com, "One Small Step For Man, One Giant Coin Flip For Mankind".
We will show that there are $12$ non-trivial solutions to the $3$-astronaut problem with $4$ coins and $2$ non-trivial solutions to the $5$-astronaut problem with $6$ coins.
Three Astronauts
The problem statement walks through the impossibility of using two coins, with $2^2=4$ outcomes, to determine a winner for three astronauts. The same can be said for three flips, which we will briefly discuss.
The key to attacking this problem for an $n$-astronaut scenario is equally distributing outcomes amongst the first $n-1$ astronauts. For the $3$-astronaut, $3$-flip case this translates to the following: among the $1$, $3$, $3$, and $1$ outcomes ($0$ heads, $1$ head, $2$ heads, and $3$ heads respectively), the first and second astronauts should have the same number each of $0$-head, $1$-head, $2$-head, and $3$-head outcomes. One possible assignment that meets this parameter is for the first and second astronauts to each have the distributions $0$, $1$, $1$, $0$, leaving the third astronaut with the distribution $1$, $1$, $1$, $1$. This is summarized in the table, below.
| 3 Heads 0 Tails | 2 Heads 1 Tail | 1 Head 2 Tails | 0 Heads 3 Tails |
|
|---|---|---|---|---|
| Astro #1 | 0 | 1 | 1 | 0 |
| Astro #2 | 0 | 1 | 1 | 0 |
| Astro #3 | 1 | 1 | 1 | 1 |
| Total | 1 | 3 | 3 | 1 |
This distribution, however, implies that the probability of flipping three heads and zero heads is both zero, a contradiction. All distributions with $3$ astronauts and $3$ coins yield similar contradictions.
There is no rigorous proof here to the claim that the first $n-1$ astronauts must have the same distribution of outcomes, but the likelihood of them having different outcomes that independently add up to a very specific fraction is highly unlikely. Further work below will show it's analogous to polynomials with different integer coefficients having an identical real root between $0$ and $1$.
We broaden our horizons to a $4$-coin solution, which has the $2^4=16$ outcomes of $1$, $4$, $6$, $4$, $1$, for $4$, $3$, $2$, $1$, and $0$ heads respectively. For three astronauts, we have significantly more ways to distribute the coin flips. For example, the first two astronauts could each be given the outcome distribution $0$, $2$, $3$, $2$, $0$, leaving $1$, $0$, $0$, $0$, $1$ for the third astronaut. This is summarized in the table, below.
| 4 Heads 0 Tails | 3 Heads 1 Tail | 2 Heads 2 Tails | 1 Head 3 Tails | 0 Heads 4 Tails |
|
|---|---|---|---|---|---|
| Astro #1 | 0 | 2 | 3 | 2 | 0 |
| Astro #2 | 0 | 2 | 3 | 2 | 0 |
| Astro #3 | 1 | 0 | 0 | 0 | 1 |
| Total | 1 | 4 | 6 | 4 | 1 |
We now have to see if a solution exists with this distribution. Let $h$ be the probability of flipping a heads, and $t=1-h$ be the probability of flipping a tails. We generate the probabilities of each flipping outcome: for $k$ heads in $n$ flips, a specific outcome (ignoring rearrangments) is $h^k t^{n-k} = h^k (1-h)^{n-k}$. Using the current example from the above table, our probability polynomial for astronaut 1 (and equivalently astronaut 2) becomes
\begin{eqnarray} 2 h^3 (1-h) + 3 h^2 (1-h)^2 + 2 h (1-h)^3 &=& \frac{1}{3} \\ -h^4 + 2h^3 -3 h^2 + 2h &=& \frac{1}{3} \end{eqnarray} $$ h = \frac{1}{6} \left( 3 \pm \sqrt{3 \left(4\sqrt{6} -9\right)} \right) \approx 0.242, 0.758 $$Therefore, we can state that one solution is with $h=.242$, the first astronaut getting assigned $2$, $3$, and $2$ each of the $3$-head, $2$-head, and $1$-head outcomes, and the third astronaut being assigned the $4$-head and $0$-head outcomes.
As an aside, it makes sense to have symmetric solutions here (that is, they add up to $1$), since we picked symmetric coefficients $2$, $3$, and $2$. We expect an asymmetric pick like $1$, $3$, $2$ to not yield symmetric solutions.
Let's generalize further to find all $3$-astronaut, $4$-coin solutions. There are $4$ outcomes with $3$ heads, so astronauts one and two could each get $0$, $1$, or $2$. Similarly they could get $0$, $1$, $2$, or $3$ and $0$, $1$, or $2$ of the $2$-head outcomes and $1$-head outcomes respectively. We need to test all of these scenarios, which we accomplish using the following code.
import numpy as np
import operator as op
from functools import reduce
from collections import namedtuple
Solution = namedtuple('Solution', 'coefficients roots')
def ncr(n, r):
"""Implementation of n choose r = n!/(r!*(n-r)!)"""
r = min(r, n-r)
numer = reduce(op.mul, range(n, n-r, -1), 1)
denom = reduce(op.mul, range(1, r+1), 1)
return numer / denom
def create_polys(num_coins):
"""Creates polynomial expansions in list form for n-1 to 1 heads"""
polys = []
for i in range(1, num_coins):
poly = []
neg = (-1)**i
for j in range(0, i+1):
poly.append(ncr(i, j) * neg)
neg *= -1
for k in range(i+1, num_coins):
poly.append(0)
polys.append(poly)
return polys
def create_coeff_limits(num_coins, num_astronauts):
"""Determines the maximum allocation of head/tail outcomes based off the number of coins and astronauts"""
coeffs = []
for i in range(1, num_coins):
coeffs.append(ncr(num_coins, i) // (num_astronauts - 1) + 1)
return coeffs
def is_valid_solution(root):
"""Checks if root is valid. Must be real and between 0 and 1."""
return np.isreal(root) and 0 < root < 1
def solve_poly(coeffs, polys, prob):
"""Generates and solves polynomials using np.roots
coeffs: list of "coefficients", i.e. multipliers for the number of out head/tail outcomes
polys: generated with create_polys
prob: the negated probability -1/num_astronauts
returns all valid solutions a list on named tuples
"""
sum_poly = []
valid_solutions = []
for degree in range(len(polys[0])):
term = 0
for j in range(len(polys)): # for each polynomial
term += coeffs[j] * polys[j][degree]
sum_poly.append(term)
sum_poly.append(prob)
ans = np.roots(sum_poly)
for root in ans:
if is_valid_solution(root):
valid_solutions.append(Solution(coeffs, root))
return valid_solutions
def main():
num_astronauts = 3
num_coins = 6
prob = -1.0/num_astronauts
polys = create_polys(num_coins)
coeff_limits = create_coeff_limits(num_coins, num_astronauts)
solutions = []
# Loop through all possible coefficient combinations
coeff_dividers = []
for i in range(1, len(coeff_limits)):
coeff_dividers.append(reduce(op.mul, coeff_limits[i:], 1))
# This helps us avoid recursion and nested for loops
for i in range(reduce(op.mul, coeff_limits, 1)):
coeffs = []
for j in range(len(coeff_dividers)):
coeffs.append((i // coeff_dividers[j]) % coeff_limits[j])
coeffs.append(i % coeff_limits[-1])
solutions += solve_poly(coeffs, polys, prob)
for solution in solutions:
print solution.coefficients, np.real(solution.roots) #strip 0.j
print "Number of solutions:", len(solutions)
if __name__ == '__main__':
main()
This code, with num_astronauts=3 and num_coins=4 yields the following 12 solutions, where the five listed values correspond to distributions with $4$, $3$, $2$, $1$, and $0$ heads respectively.
| $h$ | Astronauts 1 & 2 | Astronaut 3 |
|---|---|---|
| 0.4505 | 0, 0, 3, 2, 0 | 1, 4, 0, 0, 1 |
| 0.2861 | 0, 0, 3, 2, 0 | 1, 4, 0, 0, 1 |
| 0.6051 | 0, 1, 3, 2, 0 | 1, 2, 0, 0, 1 |
| 0.2578 | 0, 1, 3, 2, 0 | 1, 2, 0, 0, 1 |
| 0.6967 | 0, 2, 2, 2, 0 | 1, 0, 2, 0, 1 |
| 0.3033 | 0, 2, 2, 2, 0 | 1, 0, 2, 0, 1 |
| 0.7139 | 0, 2, 3, 0, 0 | 1, 0, 0, 4, 1 |
| 0.5495 | 0, 2, 3, 0, 0 | 1, 0, 0, 4, 1 |
| 0.7422 | 0, 2, 3, 1, 0 | 1, 0, 0, 2, 1 |
| 0.3949 | 0, 2, 3, 1, 0 | 1, 0, 0, 2, 1 |
| 0.7579 | 0, 2, 3, 2, 0 | 1, 0, 0, 0, 1 |
| 0.2421 | 0, 2, 3, 2, 0 | 1, 0, 0, 0, 1 |
Five Astronauts
The problem is easily generalized with the above code to higher numbers of astronauts. There are two solutions for $5$ astronauts and $6$ coins, where the seven listed values correspond to distributions with $6$, $5$, $4$, $3$, $2$, $1$, and $0$ heads respectively.
| $h$ | Astronauts 1, 2, 3, & 4 | Astronaut 5 |
|---|---|---|
| 0.4326 | 0, 1, 3, 5, 3, 1, 0 | 1, 2, 3, 0, 3, 2, 1 |
| 0.5674 | 0, 1, 3, 5, 3, 1, 0 | 1, 2, 3, 0, 3, 2, 1 |
We can also search for solutions with larger numbers of coins. The $64$ solutions for $5$ astronauts and $7$ coins are listed in the table below, where the eight listed values correspond to distributions with $7$, $6$, $5$, $4$, $3$, $2$, $1$, and $0$ heads respectively.
| $h$ | Astronauts 1, 2, 3, & 4 | Astronaut 5 |
|---|---|---|
| 0.4662 | 0, 0, 3, 8, 8, 5, 1, 0 | 1, 7, 9, 3, 3, 1, 3, 1 |
| 0.3636 | 0, 0, 3, 8, 8, 5, 1, 0 | 1, 7, 9, 3, 3, 1, 3, 1 |
| 0.4536 | 0, 0, 4, 7, 8, 5, 1, 0 | 1, 7, 5, 7, 3, 1, 3, 1 |
| 0.3863 | 0, 0, 4, 7, 8, 5, 1, 0 | 1, 7, 5, 7, 3, 1, 3, 1 |
| 0.5215 | 0, 0, 4, 8, 8, 5, 1, 0 | 1, 7, 5, 3, 3, 1, 3, 1 |
| 0.3468 | 0, 0, 4, 8, 8, 5, 1, 0 | 1, 7, 5, 3, 3, 1, 3, 1 |
| 0.527 | 0, 0, 5, 7, 8, 5, 1, 0 | 1, 7, 1, 7, 3, 1, 3, 1 |
| 0.359 | 0, 0, 5, 7, 8, 5, 1, 0 | 1, 7, 1, 7, 3, 1, 3, 1 |
| 0.5343 | 0, 0, 5, 8, 7, 5, 1, 0 | 1, 7, 1, 3, 7, 1, 3, 1 |
| 0.3845 | 0, 0, 5, 8, 7, 5, 1, 0 | 1, 7, 1, 3, 7, 1, 3, 1 |
| 0.543 | 0, 0, 5, 8, 8, 4, 1, 0 | 1, 7, 1, 3, 3, 5, 3, 1 |
| 0.4207 | 0, 0, 5, 8, 8, 4, 1, 0 | 1, 7, 1, 3, 3, 5, 3, 1 |
| 0.5513 | 0, 0, 5, 8, 8, 5, 0, 0 | 1, 7, 1, 3, 3, 1, 7, 1 |
| 0.4487 | 0, 0, 5, 8, 8, 5, 0, 0 | 1, 7, 1, 3, 3, 1, 7, 1 |
| 0.5742 | 0, 0, 5, 8, 8, 5, 1, 0 | 1, 7, 1, 3, 3, 1, 3, 1 |
| 0.3363 | 0, 0, 5, 8, 8, 5, 1, 0 | 1, 7, 1, 3, 3, 1, 3, 1 |
| 0.4564 | 0, 1, 2, 8, 8, 5, 1, 0 | 1, 3, 13, 3, 3, 1, 3, 1 |
| 0.3758 | 0, 1, 2, 8, 8, 5, 1, 0 | 1, 3, 13, 3, 3, 1, 3, 1 |
| 0.5278 | 0, 1, 3, 8, 8, 5, 1, 0 | 1, 3, 9, 3, 3, 1, 3, 1 |
| 0.3532 | 0, 1, 3, 8, 8, 5, 1, 0 | 1, 3, 9, 3, 3, 1, 3, 1 |
| 0.5376 | 0, 1, 4, 7, 8, 5, 1, 0 | 1, 3, 5, 7, 3, 1, 3, 1 |
| 0.3673 | 0, 1, 4, 7, 8, 5, 1, 0 | 1, 3, 5, 7, 3, 1, 3, 1 |
| 0.5519 | 0, 1, 4, 8, 7, 5, 1, 0 | 1, 3, 5, 3, 7, 1, 3, 1 |
| 0.396 | 0, 1, 4, 8, 7, 5, 1, 0 | 1, 3, 5, 3, 7, 1, 3, 1 |
| 0.5674 | 0, 1, 4, 8, 8, 4, 1, 0 | 1, 3, 5, 3, 3, 5, 3, 1 |
| 0.4326 | 0, 1, 4, 8, 8, 4, 1, 0 | 1, 3, 5, 3, 3, 5, 3, 1 |
| 0.5793 | 0, 1, 4, 8, 8, 5, 0, 0 | 1, 3, 5, 3, 3, 1, 7, 1 |
| 0.457 | 0, 1, 4, 8, 8, 5, 0, 0 | 1, 3, 5, 3, 3, 1, 7, 1 |
| 0.5995 | 0, 1, 4, 8, 8, 5, 1, 0 | 1, 3, 5, 3, 3, 1, 3, 1 |
| 0.3409 | 0, 1, 4, 8, 8, 5, 1, 0 | 1, 3, 5, 3, 3, 1, 3, 1 |
| 0.5566 | 0, 1, 5, 6, 8, 5, 1, 0 | 1, 3, 1, 11, 3, 1, 3, 1 |
| 0.3849 | 0, 1, 5, 6, 8, 5, 1, 0 | 1, 3, 1, 11, 3, 1, 3, 1 |
| 0.5831 | 0, 1, 5, 7, 7, 5, 1, 0 | 1, 3, 1, 7, 7, 1, 3, 1 |
| 0.4169 | 0, 1, 5, 7, 7, 5, 1, 0 | 1, 3, 1, 7, 7, 1, 3, 1 |
| 0.604 | 0, 1, 5, 7, 8, 4, 1, 0 | 1, 3, 1, 7, 3, 5, 3, 1 |
| 0.4481 | 0, 1, 5, 7, 8, 4, 1, 0 | 1, 3, 1, 7, 3, 5, 3, 1 |
| 0.6155 | 0, 1, 5, 7, 8, 5, 0, 0 | 1, 3, 1, 7, 3, 1, 7, 1 |
| 0.4657 | 0, 1, 5, 7, 8, 5, 0, 0 | 1, 3, 1, 7, 3, 1, 7, 1 |
| 0.6287 | 0, 1, 5, 7, 8, 5, 1, 0 | 1, 3, 1, 7, 3, 1, 3, 1 |
| 0.351 | 0, 1, 5, 7, 8, 5, 1, 0 | 1, 3, 1, 7, 3, 1, 3, 1 |
| 0.6151 | 0, 1, 5, 8, 6, 5, 1, 0 | 1, 3, 1, 3, 11, 1, 3, 1 |
| 0.4434 | 0, 1, 5, 8, 6, 5, 1, 0 | 1, 3, 1, 3, 11, 1, 3, 1 |
| 0.6137 | 0, 1, 5, 8, 7, 4, 0, 0 | 1, 3, 1, 3, 7, 5, 7, 1 |
| 0.5464 | 0, 1, 5, 8, 7, 4, 0, 0 | 1, 3, 1, 3, 7, 5, 7, 1 |
| 0.6327 | 0, 1, 5, 8, 7, 4, 1, 0 | 1, 3, 1, 3, 7, 5, 3, 1 |
| 0.4624 | 0, 1, 5, 8, 7, 4, 1, 0 | 1, 3, 1, 3, 7, 5, 3, 1 |
| 0.641 | 0, 1, 5, 8, 7, 5, 0, 0 | 1, 3, 1, 3, 7, 1, 7, 1 |
| 0.473 | 0, 1, 5, 8, 7, 5, 0, 0 | 1, 3, 1, 3, 7, 1, 7, 1 |
| 0.649 | 0, 1, 5, 8, 7, 5, 1, 0 | 1, 3, 1, 3, 7, 1, 3, 1 |
| 0.3713 | 0, 1, 5, 8, 7, 5, 1, 0 | 1, 3, 1, 3, 7, 1, 3, 1 |
| 0.6242 | 0, 1, 5, 8, 8, 2, 1, 0 | 1, 3, 1, 3, 3, 13, 3, 1 |
| 0.5436 | 0, 1, 5, 8, 8, 2, 1, 0 | 1, 3, 1, 3, 3, 13, 3, 1 |
| 0.6364 | 0, 1, 5, 8, 8, 3, 0, 0 | 1, 3, 1, 3, 3, 9, 7, 1 |
| 0.5338 | 0, 1, 5, 8, 8, 3, 0, 0 | 1, 3, 1, 3, 3, 9, 7, 1 |
| 0.6468 | 0, 1, 5, 8, 8, 3, 1, 0 | 1, 3, 1, 3, 3, 9, 3, 1 |
| 0.4722 | 0, 1, 5, 8, 8, 3, 1, 0 | 1, 3, 1, 3, 3, 9, 3, 1 |
| 0.6532 | 0, 1, 5, 8, 8, 4, 0, 0 | 1, 3, 1, 3, 3, 5, 7, 1 |
| 0.4785 | 0, 1, 5, 8, 8, 4, 0, 0 | 1, 3, 1, 3, 3, 5, 7, 1 |
| 0.6591 | 0, 1, 5, 8, 8, 4, 1, 0 | 1, 3, 1, 3, 3, 5, 3, 1 |
| 0.4005 | 0, 1, 5, 8, 8, 4, 1, 0 | 1, 3, 1, 3, 3, 5, 3, 1 |
| 0.6637 | 0, 1, 5, 8, 8, 5, 0, 0 | 1, 3, 1, 3, 3, 1, 7, 1 |
| 0.4258 | 0, 1, 5, 8, 8, 5, 0, 0 | 1, 3, 1, 3, 3, 1, 7, 1 |
| 0.6678 | 0, 1, 5, 8, 8, 5, 1, 0 | 1, 3, 1, 3, 3, 1, 3, 1 |
| 0.3322 | 0, 1, 5, 8, 8, 5, 1, 0 | 1, 3, 1, 3, 3, 1, 3, 1 |
Bonus: Riddler Express
The code below is an brute-force solution to the Riddler Express problem about soccer team selection. The smallest solution found was with jersey numbers $1$, $5$, $6$, $8$, $9$, $10$, $12$, $15$, $18$, $20$, and $24$.
import itertools
def brute_soccer(team_list):
average_score = sum([1./i for i in team_list])
if abs(average_score-2.0) < 1e-8:
print team_list, average_score
for i in itertools.combinations(range(1, 25), 11):
brute_soccer(i)
Efficient Item Swapping Between Nodes
Posted on April 9, 2019
Introduction
A new uniform is coming to the Air Force: the OCP (Operational Camouflage Pattern) is replacing the ABU (Airmen Battle Uniform). Despite the long-term simplicity and cost savings that stem from the Air Force and Army sharing a common uniform, a number of short-term challenges arise.
As part of the ABU's retirement, the 145 Air Force ROTC detachments across the country are being asked to trade uniform items among themselves in lieu of making new purchases, an admirable cost-saving, waste-reducing goal. So, for example, if Det 002 has three extra 'Mens 38L ABU Blouse', and Det 075 needs three of them, Det 002 could ship those three blouses to Det 075. If there were just a few items or few detachments, this exercise would be trivial. However, many detachments need hundreds of uniform items 400+ distinct uniform item types spread among the 145 detachments. The complexity grows quickly.
Given a set number of total swaps (shipments), maximize the number of transferred items (uniforms) between nodes (detachments)
A (notional) detachment may need as many 100 items from (say) 30 item types, maybe only 90 of which can be provided by other dets, and it may required shipments from (say) 7 of those detachments. If this were the case, then hundreds of shipments need to be coordinated on dynamically changing information (every shipment changes a detachment's needs and current inventory). Once you factor in the time associated with contacting other detachments, and possible second order effects like detachments underreporting overages to save effort in a brutally time-consuming process, and you are left with a exorbitantly inefficient plan doomed for failure. Greedy matching algorithms to the rescue!
More Background
Here are the problems that need to be addressed:- Incomplete/inaccurate information
- Time and resource constraints
- Lack of detachment involvement
Incomplete/inaccurate information: to tackle this, matches must either update a central database OR (much more simply), all matches must be made simultaneously using the same information. We will proceed with the latter route. To keep it simple for the user (individual detachments), they just need to fill out a highly specific spreadsheet and submit to a central planner.
Time and resource constraints: the central planner will then consolidate the data and algorithmically determine matches, then tell detachments what to send and where. This reduces the need for decentralized contact, a murky expansion of the quadratically scaling handshake problem.
Lack of detachment involvement: nothing is guaranteed to fix this without a mandate much higher than what this lowly ROTC instructor carries. The best one can do is feverishly sell the idea whilst staying out of trouble with superiors for "going rogue" with crazy outside-the-box ideas far above his pay grade.
A Basic Greedy Algorithm
We want to optimize the situation, but optimize what exactly? There are many paths here, but the best problem statement is: "given a set number of total swaps (shipments), maximize the number of transferred items (uniforms) between nodes (detachments)". This lends itself to a solution to the big picture problem, minimizing additional purchases and saving money. From there, the user can refine goals by changing the number of shipments with various inputs to analyze when diminishing returns set in.
The data structures are pretty simple:
- Inventory for each detachment will be stored in an integer array. Positive values indicate a surplus, negative imply a shortage, and $0$ is expected to be a fairly common value.
- Needs and shortages for each det will be compared and summarized in a 2D array with dimensions $n\times n$ where $n$ is the number of detachments. The row index will be the "giving" det and the column will be the "taking" det.
| Det 002 | Det 055 | Det 075 | Det 890 | |
|---|---|---|---|---|
| Det 002 | 0 | 17 | 0 | 4 |
| Det 055 | 10 | 0 | 5 | 2 |
| Det 075 | 2 | 3 | 0 | 28 |
| Det 890 | 3 | 45 | 1 | 0 |
In this example table, the 45 represents the number of uniform items the giving detachment (Det 890) can send to the receiving detachment (Det 055).
The user will set extra criteria such as a limit to the number of total shipments, then follow the following algorithm:
- Read input data (item-specific shortages and overages of each detachment)
- Generate/Update the "Give and Take" array
- Identify the maximum value of the "Give and Take" array
- Match specific items for giving and taking detachments and create the "order"
- Update inventory for the giving/taking detachments
- Write output data (shipments to make)
- Repeat steps 2-6 until exit conditions are met
In the above table, the first transfer selected would be Det 890 sending Det 055 the 45 items that Det 890 has as excess that Det 055 needs.
Note, updating the "Give and Take" array only requires modifying the row and column associated with the selected giver and taker. Implementing this would reduce runtime by a linear factor.
Set-up
First, some book-keeping. We will use a simple class for detachments. No there's no methods attached to it yet, but this project is in its infancy so let's leave our options open.
class Detachment:
def __init__(self, i):
self.number=i
self.inventory = None
Next, some basic variables, reading in the 'titles' (product descriptions), and reading in detachment inventory information.
det_nums=[1,2,3,4]
dets = []
num_dets = len(det_nums)
number_of_shipments = num_dets * 1
# Generate titles
file_name = 'det%03d.csv' % det_nums[0]
titles = read_titles(file_name)
# Read det info
for i in det_nums:
file_name = 'det%03d.csv' % i
inventory = read_csv(file_name)
det = Detachment(i)
det.inventory = inventory
dets.append(det)
The functions for 'read_titles' and 'read_csv' are pretty vanilla, so I'll leave those out (but they will be available in the full code).
We also need an array to hold the giver and taker. We generate this table with the following code:
def gen_give_take(dets):
num_items = len(dets[0].inventory)
num_dets = len(dets)
give_take = [0 for _ in range(num_dets ** 2)]
for g in range(len(dets)):
for t in range(len(dets)):
c=[]
for i in range(num_items):
if dets[g].inventory[i] <= 0 or dets[t].inventory[i] >= 0:
c.append(0)
else:
c.append(min(dets[g].inventory[i], -dets[t].inventory[i]))
give_take[g*num_dets+t] = sum(c)
return give_take
Implementation
The algorithm listed above is implemented below.
for _ in range(number_of_shipments):
# Step 2: Initialize give_take array
give_take = gen_give_take(dets) #TODO replace with an update function to save time
# Step 3: Find max value in give_take array
index = give_take.index(max(give_take))
taker = index % num_dets
giver = index // num_dets
# Steps 4-6: Make the order and update inventory
num_transferred_list=[] #order
current_order=[]
for i in range(num_items):
if dets[giver].inventory[i] <= 0 or dets[taker].inventory[i] >= 0:
num_transferred_list.append(0)
else:
num_transferred = min(dets[giver].inventory[i], -dets[taker].inventory[i])
num_transferred_list.append(num_transferred)
dets[giver].inventory[i] -= num_transferred
dets[taker].inventory[i] += num_transferred
current_order.append([titles[i], num_transferred])
Proving Optimality of the Greedy Algorithm
This is an exercise left to the reader. I wrote up a proof, but it's too lengthy to fit in the margins of this text.
Counting Sorted Matrix Permutations
Posted on January 13, 2019
Introduction
Consider an $r\times c$ matrix with unique values. It is sorted if each value is greater than the value above it and to its left. E.g. $ \begin{bmatrix} 1& 2 \\ 3 & 4 \end{bmatrix} $ and $ \begin{bmatrix} 1& 3 & 4 \\ 2 & 5 & 6 \end{bmatrix} $ are sorted, but $ \begin{bmatrix} 2& 3 \\ 1 & 4 \end{bmatrix} $ is not since $2>1$.
Our goal is to count the number of unique sorted matrices for a $r \times c$ matrix. WLOG, let the entries of the matrix be the first $n$ natural numbers, where $n=r\cdot c$. One-dimensional matrices have a trivial result; with unique entries, there is a single unique sort. The number of sorted $2\times n$ matrices will be shown to be the $n$th Catalan number, a common sequence in combinatorics.
The five $2\times 3$ (or $3\times 2$, the sorting is symmetric about the transpose) matrices are: $ \begin{bmatrix} 1& 2 & 3 \\ 4 & 5 & 6 \end{bmatrix} $, $ \begin{bmatrix} 1& 2 & 4 \\ 3 & 5 & 6 \end{bmatrix} $, $ \begin{bmatrix} 1& 2 & 5 \\ 3 & 4 & 6 \end{bmatrix} $, $ \begin{bmatrix} 1 & 3 & 4 \\ 2 & 5 & 6 \end{bmatrix} $, and $ \begin{bmatrix} 1& 3 & 5 \\ 2 & 4 & 6 \end{bmatrix} $.
This has long been a problem I wanted to work through. A simple real-life analogy is rooted in a common experience of my own (standing around in formation all day with nothing to do but ponder math problems like this): How many different arrangements of $r\cdot c$ people in a $r\times c$ rectangular formation exist such that each person is taller than the person in front of them and to their left.
Brute Force Counting
A simple algorithm can calculate all sorted permutations, but is computationally costly. The complexity for $n = r\cdot c$ rows and columns is $O(n!)$. The basic pseudo code is
def check_list(test_list, r, c):
for i in xrange(r):
for j in xrange(c):
index = c * i + j
if i > 0 and test_list[index] < test_list[index - c]:
return False
if j > 0 and test_list[index] < test_list[index - 1]:
return False
return True
In this example and all other code examples, $i$ will refer to the row and $j$ to the column. This code brute-force checks an inputted list. It is still the user's responsibility to generate the list, a task with combinatorial run time (and memory usage if implemented poorly). A simple library for generating list permutations in Python is itertools. One would check all $4\times 3$ matrices with the code.
import itertools
r, c=(4, 3)
count = 0
for test_list in itertools.permutations(range(1, r * c + 1)):
if check_list(test_list, r, c):
count += 1
Algorithmic Improvements
One does not want to check all permutations if it can be helped. It is easily observed that, for example, the point in the upper left at $(i, j)=(0, 0)$ must be $v(0, 0)=1$. Furthermore, the bottom right value at $(i, j)=(r-1, c-1)$ must be $v(r-1, c-1)=n$. How do we generalize further?
Consider an arbitrary position $(i,j)$ in the matrix. The value $v(i,j)$ must be greater than every point above and to its left, but inductively also every point to the left of those above it and above those to its left. Basically, every point in the rectangle generated $0$ to $i$ and $0$ to $j$ is less, so the minimum value of $v$ is $v_{\min}(i,j)=(i+1)\cdot(j+1)$.
Similarly, $v$ must be less than every point below and to its right, but inductively also every point to the right of those below it and below those to its right. Therefore the maximum value of $v$ is $v_{\max}(i,j)=r\cdot c-(r-i)\cdot (c-j)+1$.
In the image below, values above and to the left (in blue) must be less than $v$. Values below and to the right must be greater than $v$.
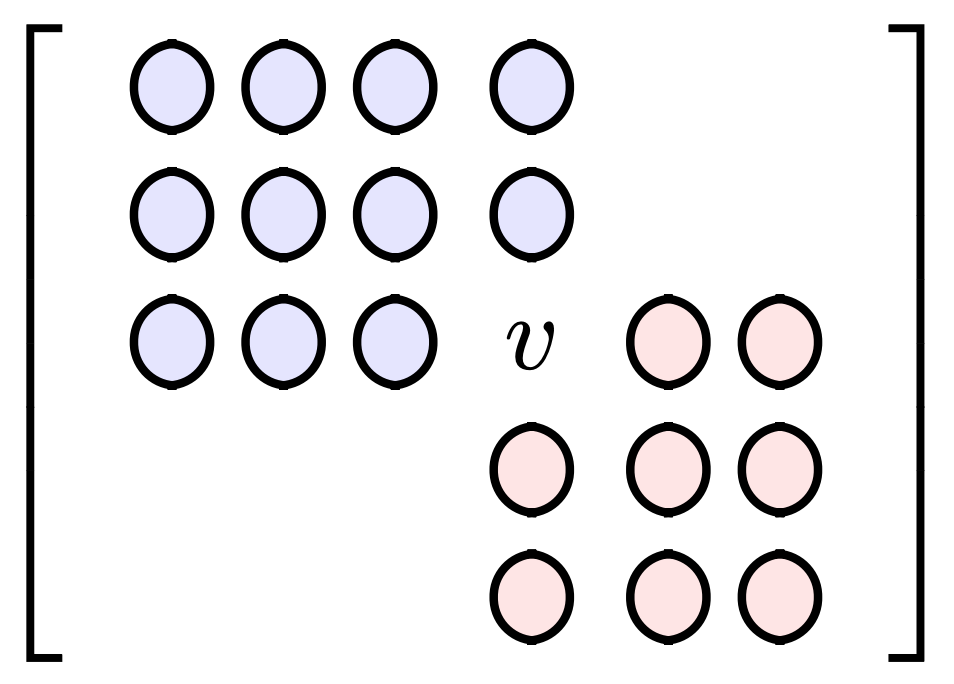
We can improve the bounds further. By the time we get to where $v$ goes, we already have the values to its left and above and those are often more restrictive than the value $(i+1)\cdot (j+1)$. Succinctly, we can improve our lower bound to be $v_{\min}(i,j)=\max\left[ v(i-1,j), v(i,j-1)\right]$.
We can also take advantage of proper data structures to further improve run time. The matrix must have unique values, so as we test values to insert into our list, we need to make sure it's not already in the list. Look-ups in arrays of length $n$ have a run time of $O(n)$. To speed up runtime, we could utilize a Python set in addition to our list, which has roughly $O(1)$ look-up time.
The fully improved code is implemented recursively below.
def recursive_check(test_list, r, c, n, s, count):
if n == r * c:
count += 1
return count
i = n // c # row
j = n % c # col
high = r*c-(r-i)*(c-j)+1
if j == 0:
low = test_list[n - c]
elif i == 0:
low = test_list[n - 1]
else:
low = max(test_list[n - c], test_list[n - 1])
for v in xrange(low, high+1):
if v in s:
continue
test_list.append(v)
s.add(v)
count = recursive_check(test_list, r, c, n + 1, s, count)
test_list.pop(-1)
s.remove(v)
return count
One would check all $4\times 3$ matrices with the code.
r, c=(4, 3)
count = 0
test_list = [1]
s = {1}
count = recursive_check(test_list, r, c, 1, s, count)
Appending and popping from a Python list is typically considered slower than preallocation and assignment, but the array sizes are small enough that the impact is negligible. Python also does it's own pre and reallocation underneath the hood. For more, check out Chapter 3 of High Performance Python.
Note, our code passes a number of variables (six in all) as input to this recursive function, which borders on sloppy. This is not the cleanest approach; one could make the variables global (not recommended), make them attributes of an object and the recursive function a method of that object, or implement a C-structure object (which in Python can be implemented with named tuple or dictionary (see here for more information on implementation). There's always more than one way to skin a cat, just make sure your code is clean.
A comparison of run times is below for a $4\times 3$ matrix in Python. The final algorithm indicates looks ups in a set instead of the original list.
| Algorithm | Run Time |
|---|---|
| Brute Force | 713.0 s |
| Bounded List Look-ups | 0.0128 s |
| Set Look-ups | 0.0101 s |
A comparison of run times is below for a $5\times 4$ matrix in Python.
| Algorithm | Run Time |
|---|---|
| Brute Force | - |
| Bounded List Look-ups | 182.0 s |
| Set Look-ups | 107.3 s |
(Multi-Dimensional) Catalan Numbers
Now that we have a decent algorithm, we can generate a table to summarize the number of sorted matrices.
| r/c | 2 | 3 | 4 | 5 |
|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 |
| 2 | 2 | 5 | 14 | 42 |
| 3 | 5 | 42 | 462 | 6,006 |
| 4 | 14 | 462 | 24,024 | 1,662,804 |
| 5 | 42 | 6,006 | 1,662,804 | 701,149,020 |
| 6 | 132 | 87,516 | 140,229,804 | - |
| 7 | 429 | 1,385,670 | - | - |
| 8 | 1,430 | 23,371,634 | - | - |
| 9 | 4,862 | - | - | - |
As was stated in the Introduction, the 2nd column (and 2nd row) immediately stick out as the Catalan numbers, which show up in all kinds of counting problems. So do the other sequences, like the $3\times n$ or $4\times n$ totals have a home? Integer sequences can be checked against the database at oeis.org. Just enter a comma-separated integer sequence and the site will determine if it's already been discovered. A little more investigation ($3\times n$ search and $4\times n$ search) uncovers the rest of the terms as Higher Dimension Catalan Numbers.
For all this, we merely rediscovered an existing set of sequences (which shouldn't surprise anyone). They have a closed form formula $$ T(m, n) = \frac{0!\cdot 1!\cdot ... \cdot (n-1)! \cdot (m\cdot n)! }{m! \cdot (m+1)! \cdot ...\cdot (m+n-1)! }. $$ Still it was a fun little adventure.
Calculating Mach Number from Schlieren Images of a Wedge
Posted on January 5, 2019
This post is going to cover the solution to a problem I solved four years ago when I worked in the wind tunnels at Wright-Patterson AFB. It’s a fun math problem that features Newton’s Method like the previous post. Put simply,
Using the top and bottom wedge and shock angles of a wedge in supersonic flow, one can calculate Mach number, even with pitch and camera angle uncertainty.
We were exploring different ways to measure or calculate Mach number in a supersonic wind tunnel. One proposed way was to measure the angles formed by oblique shocks on supersonic wedges in schlieren imagery. This is normally considered an elementary exercise, but there was concern about the fidelity of using wedge and shock angles without certainty of the pitch angle of the wedge in the tunnel or of the schlieren camera angle.
If you’re not familiar, here is an example of schlieren imagery on the SR-71’s engine inlet.

The lines in the image are shock waves. On a simple object like a wedge, the shock angle, wedge angle, and upstream and downstream Mach numbers (Mach number decreases through a shock) are all mathematically tied together. These relations are usually covered in a sophomore or junior level aerodynamics class.
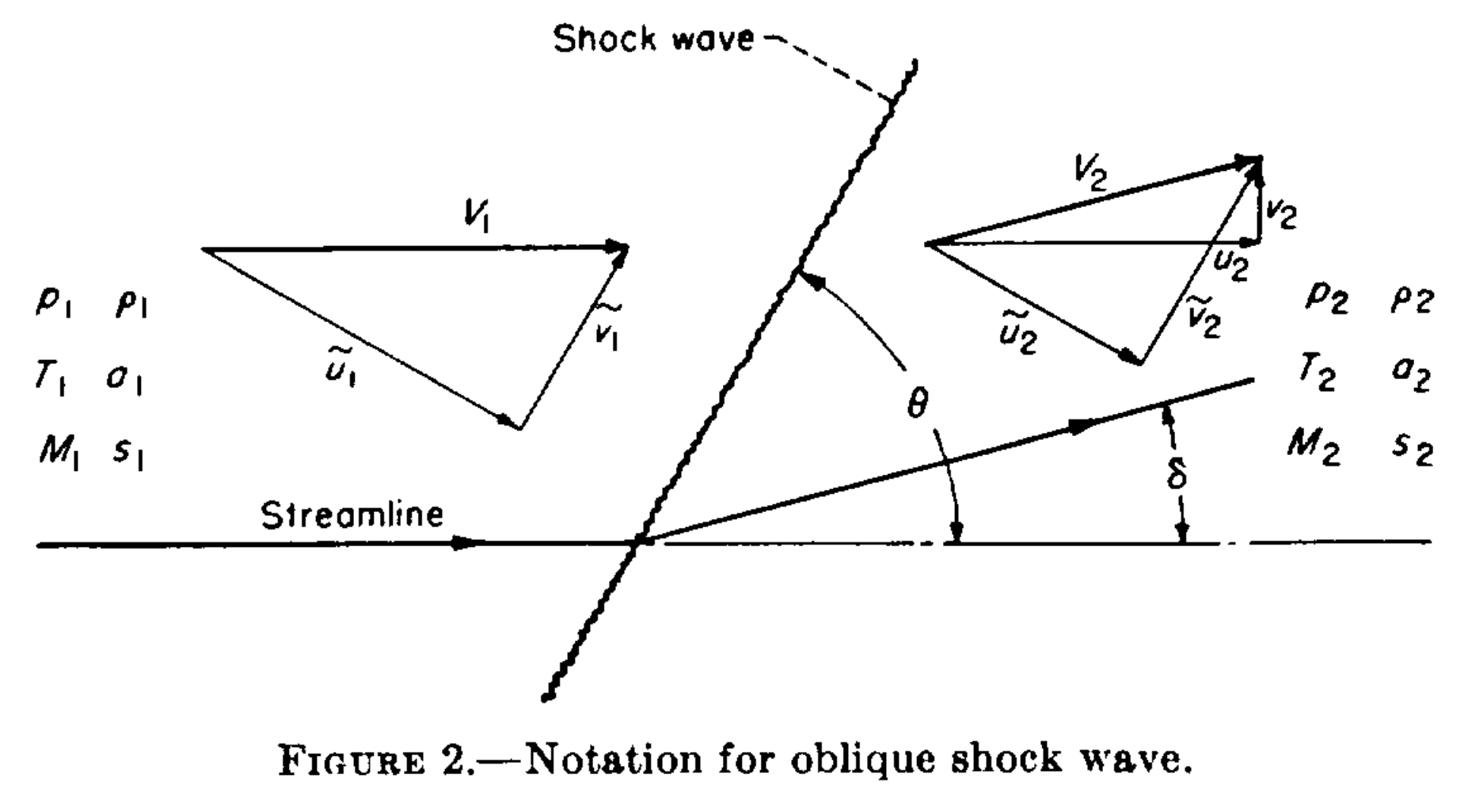
The relation is most concisely summarized in NACA Report 1135. We will adopt its terminology for simplicity. Most importantly, Mach number is $\mathrm{M}$, the wedge angle (also called half angle) is $\delta$, and the shock angle is $\theta$. Let's do a quick example to reinforce these terms.
Warm-up Exercise
Given a wedge half-angle $\delta=10^{\circ}$ and shock angle $\theta=30^{\circ}$, calculate upstream Mach number.
Warm-up Solution
Using Equation 148b on page 622 of the Report, we have
\begin{eqnarray*} \mathrm{M}_1 &=& \sqrt{ \displaystyle\frac{2(\cot{\theta}+\tan{\delta})}{\sin{2\theta}-\tan{\delta}(\gamma + \cos{2\theta})} } \\ &=& \sqrt{ \displaystyle\frac{2(\cot{30^{\circ}}+\tan{10^{\circ}})}{\sin{60^{\circ}}-\tan{10^{\circ}}(1.4 + \cos{60^{\circ}})} } \\ &=& 2.681 \end{eqnarray*}This was easy enough, but of course real life is a little more challenging.
NOTE: from here on out, we are abandoning the subscripts $1$ and $2$ for upstream and downstream, they will now refer to the top and bottom edges of a wedge.
Problem
Using upper and lower shock angles and half angles, $\theta_1$, $\delta_1$, $\theta_2$, and $\delta_2$, calculate upstream Mach number. The subscripts $1$ and $2$ refer to the angle measured on the upper and lower wedge. You cannot assume a non-zero pitch $p$ or camera deflection angle $c$, and neither are known quantities (neglect flow angularity in the tunnel).
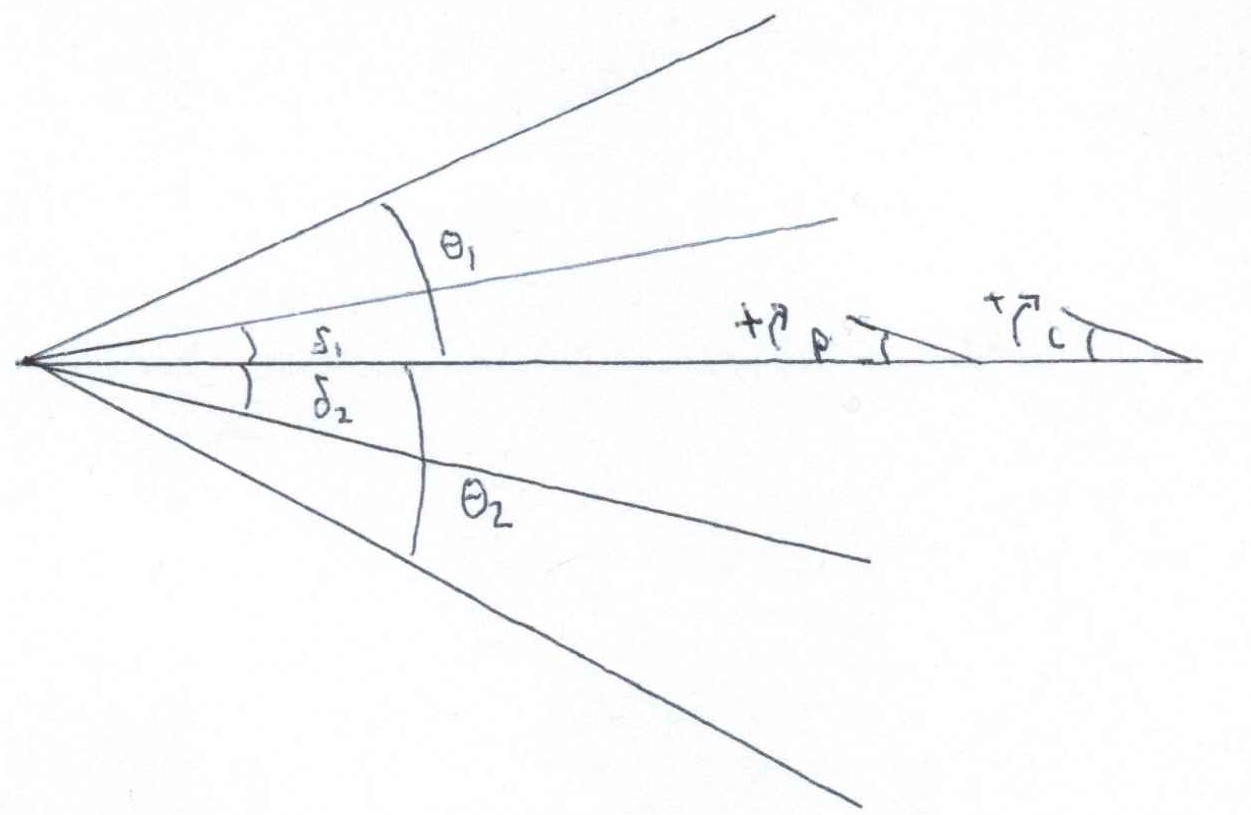
Down the Wrong Rabbit Hole
You may be first tempted to average the two deflection angles to get the half angle of the wedge. While this is simple and arguably accurate, it is not particularly helpful. There is an offset angle between them that can be caused by two (or more?) things: camera offset angle and the pitch angle of the wedge, $c$ and $p$.
Here's the problem with camera angle and pitch contributions to oblique shocks: changing the camera angle doesn't affect the physics of the shocks, but changing the pitch of the wedge does. Changing $p$ affects the effective half angle for the upper and lower wedges, thus influencing $\theta_1$ and $\theta_2$, but changing $c$ only offsets them. We need an approach that properly incorporates $c$ and $p$.
Solution
It out turns pitch angle is a sort of red herring; the solution lies in ignoring it (explcitly). Pitch is implicitly built in to the relationship between the wedge angles. That's not to say it doesn't matter, averaging the wedge angles $\delta_1$ and $\delta_2$, for example, removes the implicit pitch contribution. As long as you don't mess with the half angles, pitch is accounted for.
If it helps, think of the top and bottom as separate wedges. Then we can apply equation 148b with camera angle. By using two equations, one each for top and bottom, we implicitly account for it.
$$\mathrm{M}_{1}^2 = \displaystyle\frac{2[\cot{(\theta_1+c)}+\tan{(\delta_1+c)}]} {\sin{(2\theta_1+2c)}-\tan{(\delta_1+c)}[\gamma + \cos{(2\theta_1+2c)}]} $$ And $$ \mathrm{M}_{2}^2 = \displaystyle\frac{2[\cot{(\theta_2-c)}+\tan{(\delta_2-c)}]} {\sin{(2\theta_2-2c)}-\tan{(\delta_2-c)}[\gamma + \cos{(2\theta_2-2c)}]} $$Subtract the two equations from each other (because $M_{1}=M_{2}$) and we are left with a single equation with the single unknown $c$ (remember, $\delta_1$, $\delta_2$, $\theta_1$ and $\theta_2$ will each be measured).
This is no picnic to solve analytically, but it can be easily tackled with Newton’s method. Newton requires the function and its derivative, which can be calculated using diff in MATLAB or sympy in Python (DON'T DIY). The MATLAB is
function [c,M] = find_offset(t1,t2,d1,d2)
%// returns offset (c) and Mach number
y=1.4; %// Specific heat ratio
tol=1e-10; %// Difference required to break loop
maxiterations=1000;
c=0; %// Initial guess for offset csilon
for i=1:maxiterations
%// 1 corresponds to top edge, 2 corresponds to bottom edge
M1=2*(cot(t1+c)+tan(d1+c))/(sin(2*(t1+c))-tan(d1+c)*(y+cos(2*(t1+c))));
M2=2*(cot(t2-c)+tan(d2-c))/(sin(2*(t2-c))-tan(d2-c)*(y+cos(2*(t2-c))));
dM1=-(2*cot(c+t1)^2-2*tan(c+d1)^2)/...
(sin(2*c+2*t1)-tan(c+d1)*(cos(2*c+2*t1)+7/5)) ...
-((2*cot(c+t1)+2*tan(c+d1))*(2*cos(2*c+2*t1)+...
2*sin(2*c+2*t1)*tan(c+d1)-(tan(c+d1)^2+1)*(cos(2*c+2*t1)+7/5)))...
/(sin(2*c+2*t1)-tan(c+d1)*(cos(2*c+2*t1)+7/5))^2;
dM2=(2*cot(t2-c)^2-2*tan(d2-c)^2)...
/(sin(2*t2-2*c)-tan(d2-c)*(cos(2*t2-2*c)+7/5))+...
((2*cot(t2-c)+2*tan(d2-c))*(2*cos(2*t2-2*c)+...
2*sin(2*t2-2*c)*tan(d2-c)-(cos(2*t2-2*c)+7/5)*(tan(d2-c)^2+1)))...
/(sin(2*t2-2*c)-tan(d2-c)*(cos(2*t2-2*c)+7/5))^2;
%// Newtons Method
Mdiff=M1-M2;
dMdiff=dM1-dM2;
diff=Mdiff/dMdiff;
c=c-diff;
%// Check for early break
if abs(diff) < tol
break
end
end %// for loop
end %// function
If you're a skeptic, the alarm bells might be ringing. You can't just ignore what components factor into the offset angle...can you?
This is hard to prove (frankly I'm not sure how one would rigorously), and even a rigorous mathematical exercise would probably put the average engineer to sleep. That's in part because the approach is so counter-intuitively simple, so much so that it took me days to convince other engineers it was right. A senior engineer, late to a meeting, even left me at his desk with a blank piece of paper and a pencil and the dismissive farewell of "Try to prove to yourself why you're wrong before I come back".
In the engineering world, test cases can make a good case for the algorithm's veracity. Here is a batch of test cases. Here $\delta$ is the "original" half angle of the wedge; it is not used except to help generate test cases.
| $\mathrm{M}$ | $\delta$ | $p$ | $c$ | $\delta_1=(\delta+p)-c$ | $\delta_2=(\delta-p)+c$ | $\theta_1=\theta(\mathrm{M},\delta+p)-c$ | $\theta_2=\theta(\mathrm{M},\delta-p)+c$ |
|---|---|---|---|---|---|---|---|
| $2$ | $10^{\circ}$ | $0^{\circ}$ | $0^{\circ}$ | $10^{\circ}$ | $10^{\circ}$ | $\theta_{10}-0^{\circ}=39.31^{\circ}$ | $\theta_{10}+0^{\circ}=39.31^{\circ}$ |
| $2$ | $10^{\circ}$ | $5^{\circ}$ | $5^{\circ}$ | $10^{\circ}$ | $10^{\circ}$ | $\theta_{15}-5^{\circ}=40.34^{\circ}$ | $\theta_{5}+5^{\circ}=39.30^{\circ}$ |
| $2$ | $10^{\circ}$ | $5^{\circ}$ | $0^{\circ}$ | $15^{\circ}$ | $5^{\circ}$ | $\theta_{15}-0^{\circ}=45.34^{\circ}$ | $\theta_{5}+0^{\circ}=34.30^{\circ}$ |
| $2$ | $10^{\circ}$ | $0^{\circ}$ | $5^{\circ}$ | $5^{\circ}$ | $15^{\circ}$ | $\theta_{10}-5^{\circ}=34.31^{\circ}$ | $\theta_{10}+5^{\circ}=44.31^{\circ}$ |
| $2$ | $10^{\circ}$ | $5^{\circ}$ | $-5^{\circ}$ | $20^{\circ}$ | $0^{\circ}$ | $\theta_{15}+5^{\circ}=50.34^{\circ}$ | $\theta_{5}-5^{\circ}=29.30^{\circ}$ |
| $2$ | $10^{\circ}$ | $-5^{\circ}$ | $5^{\circ}$ | $0^{\circ}$ | $20^{\circ}$ | $\theta_{5}-5^{\circ}=29.30^{\circ}$ | $\theta_{15}+5^{\circ}=50.34^{\circ}$ |
| $2$ | $15^{\circ}$ | $-5^{\circ}$ | $5^{\circ}$ | $5^{\circ}$ | $25^{\circ}$ | $\theta_{10}-5^{\circ}=34.31^{\circ}$ | $\theta_{20}+5^{\circ}=58.42^{\circ}$ |
Here, $\theta(\mathrm{M},\delta)$ denotes a function to calculate shock angle from Mach number and wedge angle. This can be accomplished with equation 150a (the solution of which was the motivation for the previous post). The four test shock angle values are $\theta_{5}=34.30^{\circ}$, $\theta_{10}=39.31^{\circ}$, $\theta_{15}=45.34^{\circ}$, $\theta_{20}=53.42^{\circ}$.
If you write your own tests, stay away from negative and non-physical angles. Furthermore, negative angles are properly handled with Prandtl-Meyer expansion, which uses a different set of assumptions and equations.
I ran them through the code (I encourage you to do the same) and they all spit out the same Mach number, despite having either the same offset angle from different sources, or different offset angles.
If you want to run the code yourself, you can download it here. NOTE: the angles in this code are all in degrees (contrary to the snippet above).
Other Considerations
Earlier we neglected tunnel angularity. This was essential to keep our problem constrained. Solving for (one component) tunnel angularity can be achieved if we know the camera offset angle or pitch angle, but not if we know neither (and no other information). It is not a perfect substitution, but it is a simple enough exercise (and will of course be left to the reader). Depending on your setup, you may trust you camera angle more than your tunnel angularity.
Newton’s Method for Polynomials
Posted on April 14, 2018
Newton’s Methods is a useful tool for finding the roots of real-valued, differentiable functions. A drawback of the method is its dependence on the initial guess. For example, all roots of a 10th degree polynomial could be found with 10 very good guess. However, 10 very bad guesses could all point to the same root.
In this post, we will present an iterative approach that will produce all roots. Formally
Newton's method can be used recursively, with inflection points as appropriate initial guesses, to produce all roots of a polynomial.
Motivation
While working through the Aero Toolbox app, I needed to solve a particular cubic equation (equation 150 from NACA Report 1135, if you're interested).
I needed to find all 3 roots. The cubic equation is well known, but long and tedious to code up. I had already been implementing Newton’s Method elsewhere in the app and wanted to use that. The challenge though, as is always the challenge with using Newton’s Method on functions with multiple roots is robustly finding all of them.
This particular cubic was guaranteed to have three distinct roots. The highest and lowest were easy; I was solving for the square of the sine of particular angles so $0$ and $1$ are good starting points. The middle root was not so easy. After some brainstorming, I took a stab at a possible guess: the inflection point. Low and behold, it (without fail) always converged the middle root.
Delving Further
So why did the inflection point always converge to the middle root? Let's explore!
We'll start with a simple example: a polynomial with unique, real roots. The root is either identical to the inflection point, to the left of it, or to the right of it.
Assume WLOG that the derivative is positive in this region. There will always be a root in between the inflection point and the local min/max to each side (This statement requires proof, which will of course be left to the reader ;) ). Let's examine all three cases.
Case 1: Inflection Point is a root
You are at a root, so Newton's Method is converged. Both the function $p$ and its derivative $p'$ are $0$, so as long as your implementation avoids division by zero or erratic behavior close to $\frac{0}{0}$, you're in the clear.
Case 2: Root to the left of the inflection point
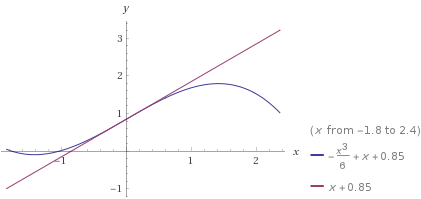
The slope will flatten out to the left of the inflection point, therefore the tangent line will intersect the $x$-axis before $p$ does. That means Newton's Method will not overshoot the root. In subsequent guesses, this same pattern will hold.
Consider an example in the graph below, $p(x)=-\frac{x^3}{6}+x+0.85$, shown in blue. In the graph below, the tangent line is shown in purple. The intersection of the tangent line and the $x$-axis is the updated guess.
Source: Wolfram Alpha
Case 3: Root to the right of the inflection point
The logic is the same, but with signs reversed. The root is to the right of the inflection point. All guesses will move right monotonically without overshooting the root.
Consider an example in the graph below of a different polynomial, $p(x)=-\frac{x^3}{6}+x-0.85$, shown in blue. In the graph below, the tangent line is shown in purple. The intersection of the tangent line and the $x$-axis is the updated guess.
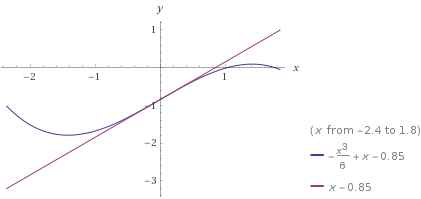
Source: Wolfram Alpha
Generalizing to Higher order Polynomials
This method can be generalized to higher orders in a recursive fashion. For an $n$th order polynomial $p$ we can use the roots 2nd derivative $p’’$ (degree $n-2$) as starting guesses for the roots of $p$. To find the roots of $p’’$, you need the roots of $p’’’’$ and so on. Also, as part of the method, you need $p’$. Therefore, all derivatives of the polynomial are required.
Two functions are required. First, a simple implementation of Newton's method
def newton_method(f, df, g, deg):
max_iterations = 100
tol = 1e-14
for i in xrange(max_iterations):
fg = sum([g ** (deg - n) * f[n] for n in xrange(len(f))])
dfg = float(sum([g ** (deg - n - 1) * df[n] for n in xrange(len(df))]))
if abs(dfg) &amp;amp;lt; 1e-200:
break
diff = fg / dfg
g -= diff
if abs(diff) &amp;amp;lt; tol:
break
return g
The second part is iteration
def roots_newton(coeff_in):
ndof = len(coeff_in)
deg = ndof - 1
coeffs = {}
roots = [([0] * row) for row in xrange(ndof)]
# Make coefficients for all derivatives
coeffs[deg] = coeff_in
for i in xrange(deg - 1, 0, -1):
coeffs[i] = [0] * (i+1)
for j in range(i+1):
coeffs[i][j] = coeffs[i + 1][j] * (i - j + 1)
# Loop through even derivatives
for i2 in xrange(ndof % 2 + 1, ndof, 2):
if i2 == 1: # Base case for odd polynomials
roots[i2][0] = -coeffs[1][1] / coeffs[1][0]
elif i2 == 2: # Base case for even polynomials
a, b, c = coeffs[2]
disc = math.sqrt(b ** 2 - 4 * a * c)
roots[2] = [(-b - disc) / (2 * a), (-b + disc) / (2 * a)]
else:
guesses = [-1000.] + roots[i2 - 2] + [1000.] #Initial guesses of +-1000
f = coeffs[i2]
df = coeffs[i2 - 1]
for i, g in enumerate(guesses):
roots[i2][i] = newton_method(f, df, g, i2)
return roots[-1]
This method will also work for polynomials with repeated roots. However, there is no mechanism for finding complex roots.
Comparison to built-in methods
The code for running these comparisons is below.#repeated roots ps = [[1, 2, 1], [1, 4, 6, 4, 1], [1, 6, 15, 20, 15, 6, 1], [1, 8, 28, 56, 70, 56, 28, 8, 1], [1, 16, 120, 560, 1820, 4368, 8008, 11440, 12870, 11440, 8008, 4368, 1820, 560, 120, 16, 1], #unique roots from difference of squares [1, 0, -1], [1, 0, -5, 0, 4], [1, 0, -14, 0, 49, 0, -36], [1, 0, -30, 0, 273, 0, -820, 0, 576], [1, 0, -204, 0, 16422, 0, -669188, 0, 14739153, 0, -173721912, 0, 1017067024, 0, -2483133696, 0, 1625702400] ] n = 1000 for p in ps: avg_newton = time_newton(p, n) avg_np = time_np(p, n) print len(p)-1, avg_newton, avg_np, avg_newton/avg_np
The comparison to built-in methods is rather laughable. A comparison to the numpy.roots subroutine is showed below. Many of the numpy routines are optimized/vectorized etc. so it isn't quite a fair comparison. Still, the implementation of Newton's Method shown here appears to have $O(n^3)$ runtime for unique roots (and higher for repeated roots), so it's not exactly a runaway success.
Two tables, below, summarize root-finding times for two polynomials. The first is for repeated roots $(x+1)^n$. The second is for unique roots, e.g. $x^2-1$, $(x^2-1)\cdot(x^2-4)$, etc.
| $n$ | Newton | np.roots | times faster |
|---|---|---|---|
| 2 | $6.10\times 10^{-6}$ | $1.41\times 10^{-4}$ | $0.0432$ |
| 4 | $5.36\times 10^{-4}$ | $1.15\times 10^{-4}$ | $4.68$ |
| 6 | $2.50\times 10^{-3}$ | $1.11\times 10^{-4}$ | $22.5$ |
| 8 | $5.54\times 10^{-3}$ | $1.23\times 10^{-4}$ | $44.9$ |
| 16 | $9.66\times 10^{-2}$ | $1.77\times 10^{-4}$ | $545.9$ |
| $n$ | Newton | np.roots | times faster |
|---|---|---|---|
| 2 | $5.57\times 10^{-6}$ | $1.03\times 10^{-4}$ | $0.0540$ |
| 4 | $2.71\times 10^{-4}$ | $1.04\times 10^{-4}$ | $2.60$ |
| 6 | $7.43\times 10^{-4}$ | $1.09\times 10^{-4}$ | $6.82$ |
| 8 | $1.43\times 10^{-3}$ | $1.21\times 10^{-4}$ | $11.8$ |
| 16 | $1.26\times 10^{-2}$ | $1.72\times 10^{-4}$ | $73.1$ |
Rearranging Digits – Brute Force Solutions
Posted on December 26, 2016
In this post we will revisit an example from the previous post Rearranging Digits with a brute force coding solution, and expand with an another example (analytically) that is trivial with with a brute force solution. The two examples are:
- Geometric Progression: Find all ordered pairs of distinct single-digit positive integers $(A, B, C)$ such that the three 3-digit positive integers $ABC$, $BCA$, and $CAB$ form a geometric progression.
- Arithmetic Progression: Find all ordered pairs of distinct single-digit positive integers $(A, B, C, D, E, F)$ such that the four 6-digit positive integers $ABCDEF$, $CDEFAB$, $FABCDE$, and $DEFABC$ form an arithmetic progression.
In the previous post we walked through a somewhat informed, yet clumsy and incomplete analytic solution that end with a less than satisfying guess and check (not to say there aren’t elegant solutions out there, I didn’t quite get there though).
This can be remedied quite easily by brute forcing our way through each of the $9^3$ possibilities for $A$, $B$, and $C$. It would look something like this in MATLAB
function [] = three_digit_with_fors()
for a=1:9
for b=1:9
for c=1:9
three_digit_geometric([a, b, c])
end
end
end
end %function
This calls the function three_digit_geometric:
function [] = three_digit_geometric(final)
tens = [100 10 1];
N1=dot(final([1 2 3]), tens);
N2=dot(final([2 3 1]), tens);
N3=dot(final([3 1 2]), tens);
if N2/N1==N3/N2 && N3~=N2
fprintf('%d, %d, %d -> ', final);
fprintf('%d, %d, %d, r=%g \n', N1, N2, N3, N3/N2);
end
end
If we wanted to generalize to higher digit numbers, the for loops would get out of hand pretty quickly, especially in with Python with forced indentation (good luck with PEP 8). To alleviate this (at least for our eyes), let’s generate a recursive function call to put these for loops in.
Now, if you’ve been around the block a bit, you know that python has itertools.permutations and MATLAB has perms – and you could use those. If you do, be wary of edge cases! The next problem is a rearrangement where some of the digits can be 0, but others are leading digits and therefore cannot. Tread lightly.
Also, perms in MATLAB appears to return the permutations in a large array (as opposed to the memory friendly generator for itertools.permutations in Python). Also, perms is recursively implemented so it’s quite easy to reach max recursive depth. Just try perms([1:n] for a large enough value of n (11 does it for me on 32-bit MATLAB 2011).
Back to our recursion. Let’s call the function rfor (short for recursive for). When given an arbitrary number of arrays, it will recursively loop through them. This will have the same shortcomings that come with any recursive algorithm, without even writing it one can posit that it will be slower and will risk reaching max recursive depth for large problems.
All of that aside, here’s what rfor would look like in MATLAB
function [] = rfor (current, final_func, level, varargin)
a=varargin;
for i=1:length(a{1})
current(level) = a{1}(i);
if length(a)>1
rfor (current, final_func, level+1, a{2:length(a)})
else
feval(final_func, current);
end
end
end
If you’re wondering whether or not time is saved by tracking the level of recursion instead of dynamically changing the size of the array, a quick benchmark showed a $>10\%$ speedup over the assignment current = [current a{1}(i)];
An example use would be
a=1:9; b=1:9; c=1:9; rfor([], 'three_digit_geometric', 1, a, b, c);
The output is
4, 3, 2 -> 432, 324, 243, r=0.75 8, 6, 4 -> 864, 648, 486, r=0.75
In case you aren't familiar with it, varargin is a way to pass a variable number of parameters to a MATLAB function. If the length is 1, we are at the lowest level of recursion required.
Python has an simple implementation as well.
def three_digit_geometric(final):
tens = [100, 10, 1]
n1 = sum([tens[i]*final[i] for i in range(len(final))])
n2 = 10 * (n1 % 100) + n1 // 100
n3 = 10 * (n2 % 100) + n2 // 100
if n2 / float(n1) == n3 / float(n2) and n3 != n2:
print n1, n2, n3, '->', final, 'r=%g' % (n3 / float(n2))
def rfor(current, final_func, level, args):
for i in args[0]:
current[level] = i
if len(args) == 1:
globals()[final_func](current)
else:
rfor(current, final_func, level+1, args[1:])
def main():
a, b, c = [range(1, 10)] * 3
rfor([0] * 3, 'three_digit_geometric', 0, [a, b, c])
As a last task, let’s solve one more fun challenge: The four six-digit numbers $ABCDEF$, $CDEFAB$, $FABCDE$, and $DEFABC$ for an arithmetic sequence. Find all possible values of ($A$, $B$, $C$, $D$, $E$, $F$).
This could probably be solved analytically. To avoid 3 equations and 6 unknowns, you would want to treat $AB$ and $DE$ as individual variables, reducing the problem to 4 unknowns (and knowledge of which should be 1-digit a 2-digit). This will be left to the reader as an exercise ;)
Here’s the code for the brute force solution (note how some digits are allowed to be zero but not others).
a=1:9; b=0:9; c=1:9; d=1:9; e=0:9; f=1:9;
rfor([], 'six_digit', a, b, c, d, e, f);
function [] = six_digit(final)
tens = [100000 10000 1000 100 10 1];
N1 = dot(final(1:6), tens);
N2 = dot(final([3:6 1:2]), tens);
N3 = dot(final([6 1:5]), tens);
N4 = dot(final([4:6 1:3]), tens);
if N2-N1==N3-N2 && N4-N3==N3-N2 && N3>N2
fprintf('%d, %d, %d, %d, %d, %d -> ', final);
fprintf('%d, %d, %d, %d, d=%d \n', N1, N2, N3, N4, N3-N2);
end
end
Here’s the output
1, 0, 2, 5, 6, 4 -> 102564, 256410, 410256, 564102, d=153846 1, 5, 3, 8, 4, 6 -> 153846, 384615, 615384, 846153, d=230769 1, 6, 2, 3, 9, 3 -> 162393, 239316, 316239, 393162, d=76923 2, 1, 3, 6, 7, 5 -> 213675, 367521, 521367, 675213, d=153846 2, 6, 4, 9, 5, 7 -> 264957, 495726, 726495, 957264, d=230769 2, 7, 3, 5, 0, 4 -> 273504, 350427, 427350, 504273, d=76923 3, 2, 4, 7, 8, 6 -> 324786, 478632, 632478, 786324, d=153846 3, 8, 4, 6, 1, 5 -> 384615, 461538, 538461, 615384, d=76923 4, 3, 5, 8, 9, 7 -> 435897, 589743, 743589, 897435, d=153846 4, 9, 5, 7, 2, 6 -> 495726, 572649, 649572, 726495, d=76923 6, 0, 6, 8, 3, 7 -> 606837, 683760, 760683, 837606, d=76923 7, 1, 7, 9, 4, 8 -> 717948, 794871, 871794, 948717, d=76923
So there are $12$ solutions.
Again if you are wondering where these came from, look no further than repeating decimals for fractions with $117$ (one of the many divisors of $999, 999$) in the denominator.
Rearranging Digits – Analytic Solutions
Posted on September 22, 2016
In this post we will work through some digit rearrangement problems.
- Six-Digit Numbers: The 6-digit number $ABCDEF$ is exactly $23/76$ times the number $BCDEFA$ (where $A$, $B$, $C$, $D$, $E$, and $F$ represent single-digit non-negative integers and $A,B>0$). What is $ABCDEF?$
- Arithmetic Progression: Find all ordered pairs of distinct single-digit positive integers $(A,B,C)$ such that the three 3-digit positive integers $ABC$, $BCA$, and $CAB$ form an arithmetic progression.
- Geometric Progression: Find all ordered pairs of distinct single-digit positive integers $(A,B,C)$ such that the three 3-digit positive integers $ABC$, $BCA$, and $CAB$ form a geometric progression.
This post will include analytic solutions, a future post will show some code-based solutions.
Six-Digit Numbers
Let's attack the first problem, repeated for clarity:
The 6-digit number $ABCDEF$ is exactly $23/76$ times the number $BCDEFA$ (where $A$, $B$, $C$, $D$, $E$, and $F$ represent single-digit non-negative integers and $A,B>0$). What is $ABCDEF?$
We will let $x=BCDEF$ be a five-digit number. Then
\begin{eqnarray*} ABCDEF &=& \frac{23}{76}\cdot BCDEFA \\ 100000\cdot A+x &=& \frac{23}{76} (10\cdot x+A) \\ 7600000\cdot A+76\cdot x &=& 230\cdot x+23\cdot A \\ 7600000\cdot A+76\cdot x &=& 230\cdot x+23\cdot A \\ 7599977\cdot A &=& 154\cdot x \\ 98701\cdot A &=& 2\cdot x \end{eqnarray*}Remember, $x$ is a five-digit integer and $A$ is a one-digit number, so one such solution is $A=2$ and $x=98701$. Are there other solutions though? Well, $A$ must be even for $x$ to be an integer, but if $A>2$ then $x$ would be a six-digit number. So there is just the one solution. As a check, this makes our numbers $ABCDEF=298701$ and $BCDEFA=987012$.
(Side note: if you are wondering where these seemingly random six-digit numbers came from, check out the repeating decimals $\frac{23}{77}$ and $\frac{76}{77}$. Fractions whose denominators are factors of $999,999$ will create repeating decimals with cycles of six digits or less and quite often use the same digits in different order.
Arithmetic Progression
Now let's look at the second problem, repeated for clarity: Find all ordered pairs of distinct single-digit positive integers $(A,B,C)$ such that the three 3-digit positive integers $ABC$, $BCA$, and $CAB$ form an arithmetic progression.
We will approach this the same way, let's define the 3 numbers \begin{eqnarray*} N_1&=&100A+10B+C \\ N_2&=&100B+10C+A \\ N_3&=&100C+10A+B \end{eqnarray*}
These terms are in arithmetic progression, which can be exploited. Let the common difference of this sequence be $d$, then \begin{eqnarray*} N_2-N_1&=& 100B+10C+A-(100A+10B+C)=d\\ N_3-N_2&=& 100C+10A+B-(100B+10C+A)= d\\ N_3-N_1&=& 100C+10A+B -(100A+10B+C)= 2d \end{eqnarray*}
After simplifying, we have \begin{eqnarray*} -99A +90B +~9C - d=0\\ ~9A -99B +90C - d =0\\ -90A ~-9B +99C - 2d =0 \end{eqnarray*}
We have a system with three equations and four unknowns, which should make you a little anxious (and the third equation is just the sum of the first two). However, if we simplify a little bit (one could do this by hand, but rref in MATLAB is our friend)
Using rref on the coefficient matrix gives us
1 0 -1 0.021021 0 1 -1 0.012012 0 0 0 0
We need integer solutions, so where do we go from here? Take a look at the two decimals, $0.\overline{021}$ and $0.\overline{012}$. The fraction equivalents are $\displaystyle\frac{7}{333}$ and $\displaystyle\frac{4}{333}$ respectively.
The equations are then \begin{eqnarray*} a-c+\frac{7}{333}d=0 \\ b-c+\frac{4}{333}d=0 \end{eqnarray*}
So if we need integers, let's get rid of the fraction by letting $d=333$. Then we have $a-c=-7$, and $b-c=-4$. This gives us the solutions $(a,b,c)=(1,4,8)$ and $(2,5,9)$. Did we get them all though? We can also let $d=-333$, which yields $a-c=7$, and $b-c=4$. This gives us the solutions $(a,b,c)=(8,5,1)$ and $(9,6,2)$.
We could try multiples of $333$ as well, but will quickly run into trouble. If $d=666$, then $a-c=14$, and $b-c=8$ but $a$ and $c$ must be single digit numbers and larger values of $d$ will violate this. We can also let $d=0$ but that just gives us the trivial solutions of an arithmetic progression with common difference $0$.
Therefore our four solutions are \begin{eqnarray*} 148,~481,~814 \\ 185,~518,~851 \\ 259,~592,~925 \\ 296,~629,~962 \\ \end{eqnarray*}
If you are wondering if these numbers came out of nowhere, check out the decimal equivalents of the $27$ths. It is no coincidence that $\displaystyle\frac{4}{27}=0.\overline{148}$, $\displaystyle\frac{13}{27}=0.\overline{481}$, and $\displaystyle\frac{22}{27}=0.\overline{814}$.
Geometric Progression
Now let's look at the last problem, again repeated for clarity: Find all ordered pairs of distinct single-digit positive integers $(A,B,C)$ such that the three 3-digit positive integers $ABC$, $BCA$, and $CAB$ form a geometric progression.
For the geomtric sequence \begin{eqnarray*} N_2-r\cdot N_1&=& 100B+10C+A-r(100A+10B+C)= 0\\ N_3-r\cdot N_2&=& 100C+10A+B-r(100B+10C+A)= 0 \end{eqnarray*}
There are other manipulations, but I haven't found any that are linearly independent of the two equations shown.
Not only do we have two equations and four unknowns, the equations are non-linear. With some simplification, we have \begin{eqnarray*} 100B+10C+A-r(100A+10B+C)= 0\\ 100C+10A+B-r(100B+10C+A)= 0 \end{eqnarray*}
Using the symbolic toolbox and rref we can simplify
% a b c [ 1, 0, (r - 10)/(10*r^2 - 1)] [ 0, 1, (r*(r - 10))/(10*r^2 - 1)]
Not incredibly helpful. However, we can reverse the columns of the array (now instead of A,B,C we have C,B,A) and rref gives us
% c b a [ 1, 0, (10*r^2 - 1)/(r - 10)] [ 0, 1, -r]
Which is a little cleaner. So where do we go from here? Well, from the last equation we have $b-ra=0 \rightarrow r=b/a$ from the second equation. So we could just try every $(a,b)$ combination ($72$ since $a\neq b$) and see if $$c=\displaystyle\frac{10r^2 - 1}{10 - r}a$$ is an integer. Still some brute force required though. You could also substitute $r=b/a$ into $c=\displaystyle\frac{10r^2 - 1}{10 - r}a$ yielding $$ c= \displaystyle\frac{10b^2-a^2}{10a - b} $$ which we just have to ensure is an integer. But again, it looks like guessing and checking is required. You could even simplify further with some polynomial division $$ c = \displaystyle\frac{10b^2-a^2}{10a - b} = \displaystyle\frac{999a^2}{10a - b} - 10b - 100a$$ which takes you down a path of finding $a$ and $b$ such that $10a - b$ is a divisor of $999a^2$, but that may even be more dangerous than guess and checking since it's so easy to leave out a case and every case must be checked to ensure $c$ is a positive single digit integer.
You can though, and it will lead you to two ordered triples, $(a,b,c)=(4,3,2)$ and $(8,6,4)$ (the second is just a less exciting multiple of the first, both have the common ratio $r=\frac{3}{4}$. The geometric series are $432,~324,~243$ and $864,~648,~486$.
This last solution left me feeling less than satisfied. In the next post we will do a code-based solution to ensure with some certainty that those are the only values.
Speeding up Code with Vectorization
Posted on January 15, 2016
In a previous post we numerically solved the heat equation with an explicit finite difference formulation, one of the simpler 2D problems in numerical analysis.
In this post we are going to speed up that computation with some vectorization. Results show we can more than double the speed of our code with some simple changes (but also that we can make it dangerously slow if implemented incorrectly).
The code examples below are in MATLAB, but you can take advantage of vectorization with other interpreted languages such as Python as well. You can read more about vectorization of MATLAB code here.
Step 1: Initialize VariablesNot much changes in this section except that we will replace nx and ny with np and use a square mesh for simplicity.
%Initialize Variables dt=.005; %time step nts=500; %number of time steps alpha=.01; %thermal diffusivity l=1; %reference length plate np=50; %number of points (x and y) dx=l/(np-1); dy=dx; %discretized distance %Temperature and derivatives stored in 2D arrays u = zeros(np); uxx = zeros(np); uyy = zeros(np);Step 2: Apply Boundary Conditions
In the following sections we will use snippets outlined in yellow to show the original code, green to show standard vectorization, and red to show sliced vectorization. In the original code (below) we looped through the two edges to apply the boundary conditions
%Boundary Conditions, original loop for i=1:np u(1,i)=1; end for i=1:np u(i,np)=1; end
This is a one-time computation so there isn’t significant time saved by changing this, but regardless we can do better by both simplifying and speeding up our code.
%Boundary Conditions, % Vectorization without slicing u(1,:)=u(1,:)+1; u(:,np)=u(:,np)+1; u(1,np)=1;
We had to correct the value of at the coordinate $(1,np)$ because are adding to it twice. So why didn’t we just take a slice of the array, like 2:np? Here is what it looks like with sliced vectorization
%Boundary Conditions, vectorization with slicing part=2:np; u(1,:)=u(1,:)+1; u(part,np)=u(part,np)+1;
This looks a little nicer, but actually has a significant impact on run time. Results of a benchmark comparison with 10,000,000 test cases is shown in the table below
| Original loop | 13.46 s |
| Vectorization with slicing | 33.29 s |
| Vectorization without slicing | 10.29 s |
So while sliced vectorization looks nice and doesn't require a correction, it more than triples execution time.
Step 3: Time LoopThe more important changes come with the code inside of the time loop, so let's shift our focus there. Here is the original code.
% Original Loop
for t=1:nts
%Calc the Spatial 2nd Derivative, Centered in Space
for i=2:np-1
for j=2:np-1
uxx(i,j)=(u(i+1,j)-2*u(i,j)+u(i-1,j))/(dx)^2;
uyy(i,j)=(u(i,j+1)-2*u(i,j)+u(i,j-1))/(dy)^2;
end
end
%Update Temperature, Forwards in Time
for i=2:np-1
for j=2:np-1
u(i,j)=u(i,j)+alpha*(uxx(i,j)+uyy(i,j))*dt;
end
end
end
We can simplify this code greatly with vectorization. The code below requires corrections, but improves run time drastically.
% Vectorization without slicing
for t=1:nts
%Calc the Spatial 2nd Derivative, Centered in Space
for i=2:np-1
uxx(i,:)=(u(i+1,:)-2*u(i,:)+u(i-1,:))/(dx)^2;
uyy(:,i)=(u(:,i+1)-2*u(:,i)+u(:,i-1))/(dy)^2;
end
uxx(2,1)=0; %correction
uyy(np,np-1)=0; %correction
% Note, we do not need to correct other BC points since the uxx,uyy=0 - it would be safer to tho
%Update Temperature, Forwards in Time
u=u+alpha*(uxx+uyy)*dt;
end
Note that we had to once again make a correction after the vectorized calculations. Here is what it looks like with sliced vectorization that wouldn't require corrections
% Vectorization with slicing
part=2:np-1;
for t=1:nts
%Calc the Spatial 2nd Derivative, Centered in Space
for i=2:np-1
uxx(i,part)=(u(i+1,part)-2*u(i,part)+u(i-1,part))/(dx)^2;
uyy(part,i)=(u(part,i+1)-2*u(part,i)+u(part,i-1))/(dy)^2;
end
%Update Temperature, Forwards in Time
u=u+alpha*(uxx+uyy)*dt;
end
Once again this looks much nicer but as we see below, the slices are once again much slower.
The comparison of all three methods run 30 times with 5000 time steps each are shown in the following table.
| Original loop | 25.48 s |
| Vectorization with slicing | 84.31 s |
| Vectorization without slicing | 10.68 s |
With properly implemented vectorization we can drastically speed up our code, but as the results show it must be done carefully and tested to ensure both accuracy (by making the proper corrections) and speed.
Drafting Fantasy Football Teams: A Comparison Greedy Algorithms
Posted on September 7, 2015
Fantasy football is an increasingly popular game for American football fans. Coaches compete within a league, typically of friends or coworkers. The standard roster of starters includes 1 QB, 2 RB, 2 WR, 1 TE, 1 D/ST (defense/special teams), 1 K, and 1 F (flex: can usually be a WR, RB, or TE). Teams also have bench players (backups for when starters are struggling or on a bye week).
If you aren’t familiar with how fantasy football works, read more here. Even if you aren’t a big football fan, this is worth learning for the exciting strategy behind playing. From here on out, I will assume you have a basic working knowledge of the game.
There are a lot of week to week strategies that coaches employ to pick up the best players off the waiver wire or win week to week, but for now we will just focus on the draft.
Simple Greedy Algorithm
The simplest way to draft is to just pick the best available player. We will call this a greedy algorithm. There is no negative connotation implied here; it just describes the algorithm design: pick the best player available based on projected points.As it turns out, this strategy isn’t too bad; better than wonky strategies like picking only Jets and Chargers players or only from teams capable of flight (both are strategies I've drafted against). Success in a draft is obviously not guaranteed. After all, only one person can draft the best team. As many seasoned coaches suspect, the lucky coaches with early picks (1-3 overall) are more likely to draft teams with the highest projections.
If you are the poor guy sitting in the back with the last pick, it seems like there’s nothing you can do. Even if you know who your opponents are picking, there is not a clear and intuitive way to leverage that information if you stick to just picking the best available. If only there was a way to take advantage of the knowledge of who other players are picking…and that’s where the predictive greedy algorithm comes in.
Predictive Greedy Algorithm
Let’s think through a modification of the simple greedy algorithm by considering the following situation. Let’s say (hypothetically) that you have the QB and WR positions open. Also, Peyton Manning is the best player available and he is worth 500 points, the next best player available is Calvin Johnson, projected to get 475 points. The simple greedy algorithm would tell you to pick Peyton because he is worth more points. When the next round comes around, Calvin Johnson is no longer available at WR so you have to “settle” on 375 from Brandon Marshall.But wait, there’s more! Let’s also say 3 spots behind Peyton (in QBs) is Philip Rivers, a less popular choice, but still projected to get 425 points. And better yet, you know how you’re opponents pick so you know there is a high chance he’ll be available next round. So you can let Peyton Manning go to another team and pick up Calvin Johnson even though he doesn’t have the highest points available, then get Phillip Rivers the next round(Peyton will surely be gone). Some simple math later, you drafted two players worth a combined 475+425=900 points (Johnson and Rivers) instead of 500+375=875 (Manning and Marshall), because you were able to predict what your opponents were going to do, and exploited it.
With that example in mind, let's formally define our new greedy algorithm. Each pick you will follow these steps:
- Determine the best available player and simulate that you pick him
- Determine the best available player at every other position
- Simulate other coaches picking for a round until the pick comes back to you
- Once again, determine the best available player at every position
- Calculate the position with the highest decrease in points and pick that player
There are some obvious shortcomings to this highly trivialized situation, namely the lack of information. You will never know exactly who you’re opponents are going to pick, and risking big by drafting lower rated players earlier can be dangerous. However, in our academically predictable environment, this strategy proves to be quite fruitful.
Comparison
We are going to simulate 66 different drafts: 6-16 person leagues (by 2’s) with everyone picking with the simple greedy strategy except for one person, who will pick with the predictive greedy algorithm. The code is largely unexciting bookkeeping so I won’t walk through it, but you can find it on GitHub.
As expected, the predictive greedy algorithm is quite successful, particularly in larger drafts and for players in the middle of the draft order.
Coaches who picked following this strategy picked the team with the highest projected points 89% of the time.
Other Considerations
This is obviously a drastic oversimplification of the drafting problem, namely because we know our opponents strategy. In reality, coaches’ picks are more sporadic. Some coaches employ strategies like picking 3 RBs in their first 3 rounds, others pick players heavily from their favorite teams.Regardless of how your league tends to pick, a key to success is to get out front of these trends right before they happen (and not too early). We can see the importance of this in the chart below.
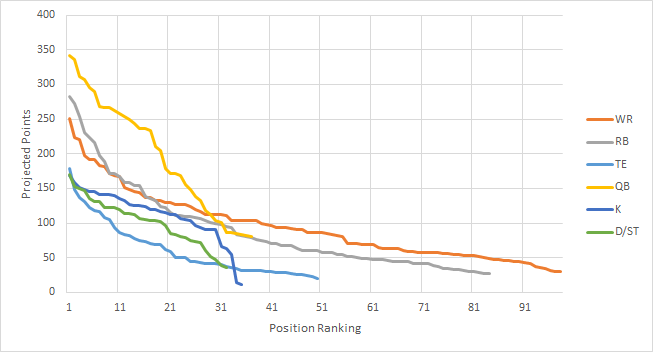
Each position has diminishing point value (the slope flattens out) as you go further out in the rankings, some faster than others. You want to pick anytime when the slope is steep, but on the front end (you don't want to pick after the major drop offs). But not all positions are picked at the same time, and this varies by league. In some leagues, quarterbacks go in the 1st round, in some not till the 5th - some leagues pick defenses in the 5th round and some pick defenses in the 8th round. If you know other coach's tendencies, you can get out in front of these major drop offs and take advantage of them.
This overlooks a few other important details - one of which is the bye week problem. Each player has a bye week some time from Week 4 to Week 11 in the 17 week season. Some coaches hedge against this by spreading out the bye weeks among their team – others try to get all the bye weeks at the same time so their team takes only one bad loss.
Another overlooked assumption comes from picking bench players. Consider a 6-team league. There are far more than six QBs that are fairly evenly matched and good enough to start on a fantasy team. Therefore in this simulation, a coach who waits until the last pick to draft the QB does not suffer too much in points lost. However, in reality, some coaches pick their backup QB quite early; some even draft a backup before they fill in all of their starting positions. This decision-making process is hard to predict in these simulations.
With all the assumptions that have gone into this analysis, it’s unlikely that a coach could replicate this success without a little bit of luck and lot of predictable behavior from their opponents. If you did have this information (looking at you ESPN), there is a lot of potential to take this in exciting new directions.
More Approximations for Trigonometric Functions with the Binomial Series
Posted on August 31, 2015
In this post, we will create a new set of approximations for sine and cosine that utilize the binomial series. Before you go any further, you may want to read this previous post where we walk through the binomial series and comparisons to the Maclaurin series.
Derivation
We are going to exploit Euler's formula with a twist. To refresh your memory, here's Euler's Formula. \begin{equation} \cos(\theta)+i\sin(\theta)=e^{i\theta} \end{equation} Now let's employ one of the older tricks in the book, adding and subtracting one from the same expression: \begin{equation} \cos(\theta)+i\sin(\theta)=\left[(e-1)+1\right]^{i\theta}. \end{equation} Now we have a binomial raised to a power. Once again, we will use known values and the binomial series to generate approximations for sine and cosine.
Fine Tuning For Approximation
In its current form this would almost be enough for decent approximations. However, closely tied to the accuracy of an approximation is the convergence rate of the series. To improve convergence, we want to make one of the terms small relative to the other term. Is there anything we can do here?
As a matter of fact, yes. We will employ a second manipulation - multiplying and dividing by the same number (inside and outside of the parentheses). Consider the updated equation \begin{equation} \cos(\theta)+i\sin(\theta)=a^i\cdot\left[\left(\displaystyle\frac{e}{a^{1/\theta}}-1\right)+1\right]^{i\theta}. \end{equation} If you need to, convince yourself that this is still valid. Now, to build a valid approximation, we need $\displaystyle\frac{e}{a^{1/\theta}}-1$ to be small for a range of values. In our previous post, we determined that you need a range of $\pi/4$ for sine and cosine, which could be extrapolated out to encompass all values.
Ideally we would just pick the range $[0,\pi/4]$, with which a value of $a=e^{\pi/8}$ would be a good place to center the approximation. However, If $\theta=0$, the expression \begin{equation} {(e^{\pi/8})^{1/0}}-1 \end{equation} is not defined (although the limit appears to exist).
On the other side of the range, at $\theta=\pi/4$, the expression becomes \begin{equation} \displaystyle\frac{e}{(e^{\pi/8})^{4/\pi}}-1=e^{1/2}-1\approx.64 \end{equation} which is enough for convergence, but maybe not optimal.
On the other hand, if we made the range $[2\pi,2\pi+\pi/4]$ with $a=2\pi+\pi/8$, then our bounding values are roughly $\approx\pm.06$ which will give us much better convergence. Due to the nature of this equation, rapidly increasing our range - for example, the range $[100\pi,100\pi+\pi/4]$ - has rapidly diminishing gains, and improved convergence will be offset by roundoff error elsewhere.
Implementing Approximations
An example of this code is (written for MATLAB) is
iterations=14;
start=2*pi;
range=pi/4;
increment=.001;
theta=start:increment:(start+range);
a=exp(start+range/2);
z=1i.*theta;
w=exp(1)./a.^(1./theta)-1;
approx=zeros(1,length(theta));
for i=iterations:-1:1
approx=1+approx.*(w.*(z-i+1)/i);
end
approx=approx*a.^(1i);
You can plot the error with the following code
error=real(approx)-cos(theta);
figure;
h=semilogy(theta,abs(error));
outfilename=sprintf('cos_error_%d_iter',iterations);
saveas(h, outfilename, 'png');
error=imag(approx)-sin(theta);
figure;
h=semilogy(theta,abs(error));
outfilename=sprintf('sin_error_%d_iter',iterations);
saveas(h, outfilename, 'png');
Error Plots
See below for the error for approximations for cosine with 4, 8, 12, and 14 terms. With 14 terms, we are more or less bounded by machine precision (~15 significant figures)
Once again we have generated some exciting looking, but nonetheless useless approximations. We were able to use binomial theorem and some trickery to generate approximations with great accuracy, but once again they are nowhere near as speedy to calculate as the Maclaurin series.
Representing Trigonometric Functions with the Binomial Series
Posted on April 4, 2014
In this post, we will introduce the incredibly useful binomial theorem and series, then use the series and De Moivre's theorem to derive a representation and approximations for trigonometric functions.
Background
The binomial theorem is a way to expand a binomial raised to a power. For a natural number $n \in \mathbb{N}$ the binomial theorem is $$ (a+b)^n={n \choose 0} a^n b^0 + {n \choose 1} a^{n-1}b+{n \choose 2} a^{n-2}b^2…+{n \choose n} a^0 b^{n}.$$
A tidier closed form expression is $$ (a+b)^n=\sum_{k=0}^{n}{ {n \choose k} a^{n-k}b^{k} } .$$ Closely related to the binomial theorem (integer exponents) is the binomial series (for non-integer exponents).
For a real exponent $\alpha \in \mathbb{R}$ the binomial theorem becomes: $$ (a+b)^{\alpha}=\sum_{k=0}^{\infty}{ {\alpha \choose k} a^{\alpha-k}b^{k} } .$$ Without getting too in depth on convergence, it is important that $a<b$. The convergence of this series when $a=b$ depends on $\alpha$. There is more on convergence here.
Even if $\alpha$ isn't an integer, the coefficients ${ \alpha \choose k}$ are calculated similarly. Let’s look at two examples.
For integers: $${ 7 \choose 3}=\frac{7\cdot 6\cdot 5}{3\cdot 2\cdot 1}=35.$$ For non-integers: $${ 7.2 \choose 3}=\frac{7.2\cdot 6.2\cdot 5.2}{3\cdot 2\cdot 1}=38.688.$$ The generalized binomial has some useful applications like approximating roots, deriving multiple angle formulas, and approximating $e$.
Deriving a series
The starting point for deriving these series is De Moivre's Theorem. The theorem is most commonly in used complex analysis, but it is probably best known as a tool for deriving multiple angle formulas. This theorem can be found in any complex analysis text, but we will state it here for clarity.
De Moivre's Theorem: For $n\in \mathbb{Z}$ and $\phi \in \mathbb{R}$
In multiple angle formula derivations, $n$ is generally a constant integer and $\phi$ is a variable. However, there are two significant differences in our approximations. We will leave $\phi$ constant and we will replace $n$ with a variable $\alpha \in \mathbb{R}$ that can vary.
In general, De Moivre's Theorem breaks down when generalized to $\alpha \in \mathbb{R}$. Any standard complex analysis book can provide examples of this. The proof is a little dry so we won’t show it here, but It can be shown that as long as we pick $\phi \in (-\pi,\pi]$, our generalization of De Moivre's Theorem holds.
Let $\phi \in (-\pi,\pi]$ with $\phi \neq 0$ and let $\theta=\alpha\phi$ for $\alpha \in \mathbb{R}$. Now we can take this special case of De Moivre's Theorem and apply the generalized binomial theorem, yielding: \begin{eqnarray*} \cos{\theta}+i\sin{\theta}&=&\cos{\alpha\phi}+i\sin{\alpha\phi}\\ &=&(\cos{\phi}+i\sin{\phi})^\alpha \\ &=&\displaystyle\sum_{k=0}^\infty{i^k{\alpha\choose k}\cos^{\alpha-k}{\phi}\sin^{k}{\phi} } \\ &=&\cos^{\alpha}{\phi}\displaystyle\sum_{k=0}^\infty{i^k{\alpha\choose k}\tan^{k}{\phi} }\\ &=&\cos^{\alpha}{\phi}\displaystyle\sum_{k=0}^\infty{(-1)^k\left[{\alpha\choose 2k}\tan^{2k}{\phi}+ i{\alpha \choose 2k+1}\tan^{2k}{\phi}\right]}. \end{eqnarray*} Now we equate the real and imaginary parts: \begin{eqnarray*} \cos{\theta}&=&\cos^{\alpha}{\phi}\displaystyle\sum_{k=0}^\infty{(-1)^k{\alpha\choose 2k}\tan^{2k}{\phi} } \\ \sin{\theta}&=&\cos^{\alpha}{\phi}\displaystyle\sum_{k=0}^\infty{(-1)^k{\alpha \choose 2k+1}\tan^{2k+1}{\phi} }. \end{eqnarray*} We can also create an alternative form by letting $x=\tan\phi \rightarrow \cos\phi=1/\sqrt{1+x^2}$: \begin{eqnarray*} \cos{\theta}&=&\left(1+x^2\right)^{-\alpha/2}\displaystyle\sum_{k=0}^\infty{(-1)^k{\alpha\choose 2k}x^{2k} } \\ \sin{\theta}&=&\left(1+x^2\right)^{-\alpha/2}\displaystyle\sum_{k=0}^\infty{(-1)^k{\alpha \choose 2k+1}x^{2k+1} }. \end{eqnarray*} While we will not go in depth here, it is important to study the convergence of these series. As a general rule, the series will converge for $\phi$ such that $\cos{\phi}>\sin{\phi}$ (this can be verified with the ratio test). It can also be shown with the alternating series test that if $\cos{\phi}=\sin{\phi}$, then the series will converge for $\theta\geq-\pi/4$. Both series converge for the values of $\theta$ and $\phi$ chosen later in this paper.
Approximations
To implement these series as approximations, they must be truncated. The error associated with this truncation is heavily dependent on both $n$, the number of terms in the truncated series, and the value of $\phi$. The number of terms will be predetermined for consistency and computational efficiency. Realistically, values around $n=8$ are a good starting place because the standard approximation for trigonometric functions in MATLAB utilizes a truncated and slightly modified Maclaurin series with $8$ terms.
For the approximations to be repeatable without re-evaluating $\tan{\phi}$ and $\cos{\phi}$, the value of $\phi$ must be constant. With $\phi$ and $n$ constant, $\alpha$ will be recomputed for each $\theta$. Sensitivity studies on $\phi$ showed that approximations with $\tan{\phi}=.1$ are exceptionally accurate for a small number of terms, so that value will be used for approximations throughout the rest of the paper. Let’s try an example.
Example: Approximate $\cos{\pi/3}$.
Solution:Let $\phi=\tan^{-1}({.1})\approx.0997$. Then we compute $\alpha = \frac{\pi/3}{.0997} = 10.5.$ We will use $n=8$ terms in our approximation. We have \begin{eqnarray*} \cos{\pi/3} &\approx& \cos^{10.5}({.0997}) \displaystyle\sum_{k=0}^7{(-1)^k{10.5 \choose 2k}\tan^{2k}({.0997})} \\ &=&\cos^{10.5}({.0997}) \left[ 1-\frac{10.5(10.5-1)}{2!}.1^2+-... \ +-\frac{10.5(10.5-1)...(10.5-13)}{14!}.1^{14} \right] \\ &=&0.49999999999999944.\\ \end{eqnarray*} These approximations cannot be easily evaluated by hand, but can be carried out with a computer quickly and with exceptional accuracy. The outline and basic code for the cosine approximation are below.
- Specify $\phi$ and $n$
- Compute $\alpha$
- Initialize coefficient and sum variables
- Use an iterative loop to calculate the generalized binomial coefficients and new terms
- Multiply the sum by $\cos^\alpha(\phi)$
An example of this code is (written for MATLAB) is
[approx, error] = function calculate_theta(theta)
tan_phi=.1;
phi=0.099668652491162;
cos_phi=0.995037190209989;
alpha=theta/phi;
coeff=1;
n=8;
sum=0;
for i=1:n
sum=sum+coeff;
coeff=-tan_phi^2*coeff*(alpha-2*i+1)*(alpha-2*i+2)/(2*i)/(2*i-1);
end
approx=sum*cos_phi^alpha;
error=approx-cos(theta);
Recall, $\phi$ is predetermined, so $\tan{\phi}$ and $\cos{\phi}$ are constants. In this code, they are represented with tan_phi and cos_phi respectively. Also, theta represents $\theta$, alpha represents $\alpha$, n represents the number of terms in the truncated series, coeff is each term in the series, and sum is utilized in the loop to add up the terms.
Before we get too ahead of ourselves, we need to consider how this stacks up against existing approximations for trigonometric functions. The simplest is the Maclaurin Series, with example source code shown here. While our approximations are a novel new look, they take much longer to compute so they are not a viable replacement for any existing approximations.
Implicit finite difference formulation on an unstructured mesh
Posted on March 17, 2014
Introduction
Objective: Obtain a numerical solution for the 2D Heat Equation using an implicit finite difference formulation on an unstructured mesh in MATLAB. The temperature distribution over time for an example problem described below will look something like this:
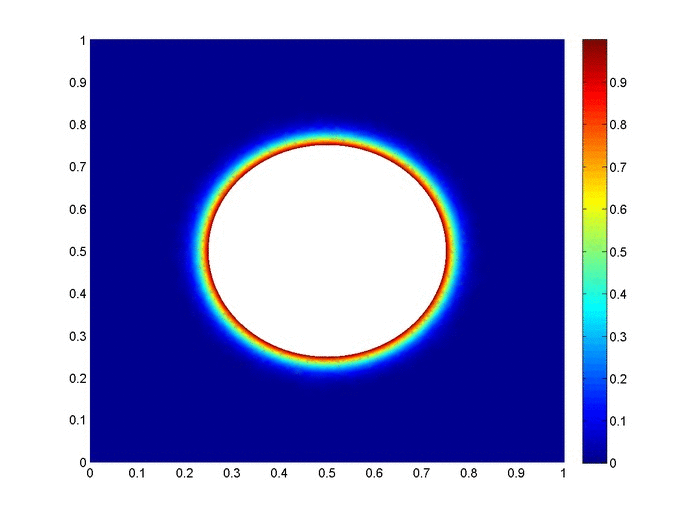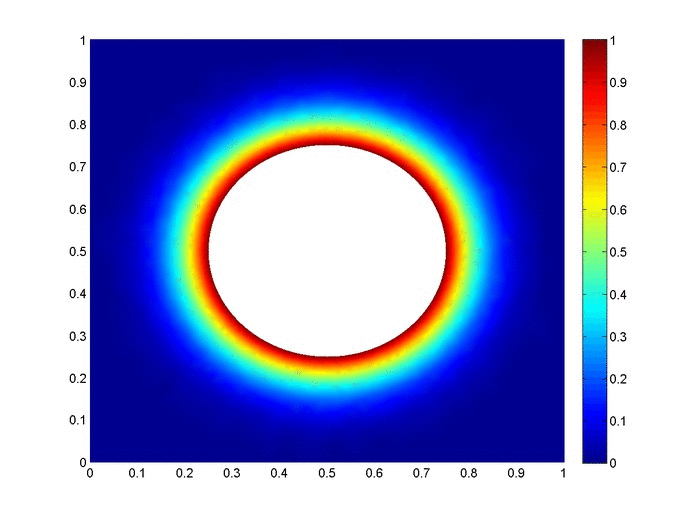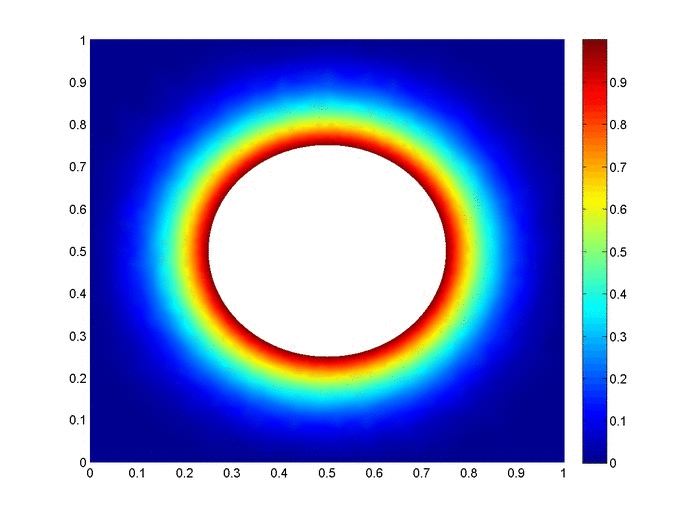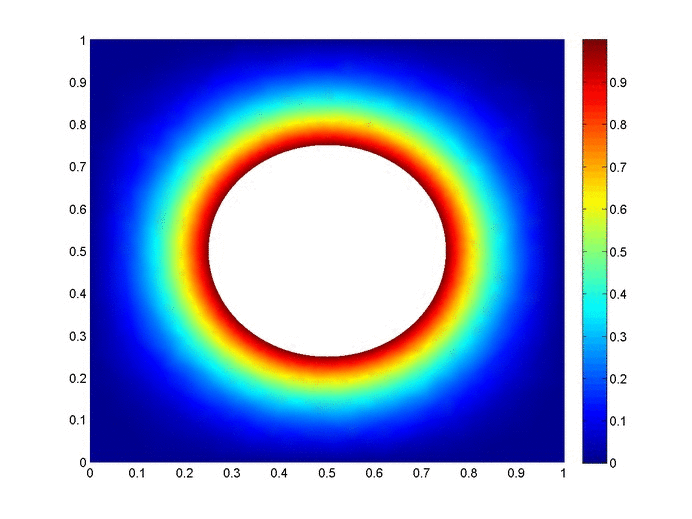
Helpful background: basic understanding of PDEs (partial differential equations), basic MATLAB coding (for loops, arrays and structure arrays), and solution methods for matrix equations.
Modeling the physics
First let’s introduce the heat equation. The heat equation in two dimensions is $$u_t=\alpha(u_{xx}+u_{yy})$$ where $u(x,y,t)$ is a function describing temperature and $\alpha$ is thermal diffusivity.
Numerically discretizing the equations We are going to solve the heat equation numerically with finite differences on an unstructured mesh. This is a fairly non-standard approach; when numerical analysts encounter difficult geometries they typically move on from cartesian finite difference for coordinate transformations, or other methods like finite volumes or finite elements on unstructured meshes.
We will keep as close as possible to the true nature of finite difference without using coordinate transformations. Our previous post did this as well, but what makes this method more desirable is the flexibility that comes from unstructured meshing. With an unstructured mesh, it is easier to mesh around complex geometries and add local refinement.
Approximating derivatives To create discretized equations we will need approximations for the second derivatives $u_{xx}$ and $u_{yy}$. We will go back to a Taylor series expansion, but this time extend it in in two dimensions. Consider a function $u$ at points $u_0=u(x_0,y_0)$ and $u_1=u(x_1,y_1)$ with $x_1=x_0+\Delta x$ and $y_1=y_0+\Delta y$. Then the two dimensional Taylor series expansion is $$ u_1 \approx u_0 + u_x\Delta x +u_y\Delta y +u_{xx}\Delta x^2 +u_{yy}\Delta y^2 +u_{xy}\Delta x \Delta y $$ We will treat $\Delta x$, $\Delta y$, $\Delta x^2$, $\Delta y^2$, $\Delta x\Delta y$, as coefficients and let the derivatives be the unknowns. Then we have a linear equation with five unknowns, $u_x$, $u_y$, $u_{xx}$, $u_{yy}$, and $u_{xy}$. That means to solve for all first and second derivatives requires five linearly independent equations, which we can get if we have $n \geq 5$ neighboring points that aren't collinear in the same direction.
Set it up as $A\textbf{x}=\textbf{b}$ where \[ \textbf{b} = \left[ \begin{array}{c} u_1-u_0 \\ u_2-u_0 \\ … \\ u_n-u_0 \end{array} \right] \] \[ \textbf{x} = \left[ \begin{array}{c} u_x \\ u_y \\ u_{xx} \\ u_{yy} \\ u_{xy} \\ \end{array} \right] \]
and $A$ is the coefficient matrix.
As one might guess, this results in approximations with second order accuracy for the first derivatives but only first order accuracy for the second derivatives, which is not acceptable accuracy. There are different ways to address this but the simplest is to add the third derivative terms to our equations. There are four third derivatives $u_{xxx}$, $u_{yyy}$, $u_{xxy}$, and $u_{xyy}$. This means we will need to use information from nine neighboring points to attain second order accuracy.
Now you may be wondering, how will we pick the nine neighboring points that best solve the physical problem? To best capture the physics we want equal weight from the surrounding points. However, unstructured meshes have a varying number of neighboring points, and often times have less than nine. To address this problem we will get greedy - we will not take just all neighboring points, but all the neighbors of neighboring points. This will leave us with much more than nine equations (generally 20-30) for only nine unknowns.
To best solve the overdetermined system we will use the least squares method. For an overdetermined system $A\textbf{x}=\textbf{b}$ the least squares solution is $$ \textbf{x}=\left[ (A^TA)^{-1}A^T \right] \textbf{b}$$ Let $\textbf{d}$ be the sum of the fourth and fifth rows of $(A^TA)^{-1}A^T$. Then we can write $$ (u_{xx}+u_{yy})_{x_0,y_0} = \textbf{d}\textbf{b}.$$ Since the mesh does not move we can use the same coefficients to calculate derivatives at every time step. Therefore these least squares calculations and assembly $\textbf{d}$ vectors (one for each node) of only need to be carried out once.
As we will show later in the code it is not good if the matrix has linearly dependent rows. To avoid this one could add an error check that eliminates $\Delta x$ and $\Delta y$ pairs that have close to the same angle. The closer points are to being linearly independent, the worse the condition of the matrix $A$. That said, if the angles differ by $180^{\circ}$ then rows are still linearly independent due to the nature of the coefficients.
Now that we have a way to calculate the derivatives, we can implement a formulation. We have shown the explicit FTCS formulation in two previous posts, so in this post we will just focus on an implicit method. We will use the Crank-Nicolson method (for more, check this paper on finite differences with the heat equation).
Implicit formulation (Crank-Nicolson)
The approximation becomes \begin{eqnarray} u_t^n &=& \alpha\cdot(u_{xx}+u_{yy}) \\ \frac{u^{n+1}-u^n}{dt} &=& \frac{\alpha}{2} \left[ (u_{xx}+u_{yy})^{n+1} + (u_{xx}+u_{yy})^n \right] \\ u^{n+1} - \frac{\alpha\cdot dt}{2}(u_{xx}+u_{yy})^{n+1} &=& u^n + \frac{\alpha\cdot dt}{2}(u_{xx}+u_{yy})^n \\ u^{n+1} - \frac{\alpha\cdot dt}{2} \textbf{d}\textbf{b}^{n+1} &=& u^n + \frac{\alpha\cdot dt}{2} \textbf{d}\textbf{b}^n \end{eqnarray} The left hand side of the equation is called the implicit side and contains the unknowns $u^{n+1}$ and $\textbf{b}^{n+1}$. The right hand side is all known values ($u^n$ and $\textbf{b}^n$ are from the previous time step) and is called the explicit side.
If we create an equation like this for each of the $n$ point in our domain then we have a system of $n$ equations with $n$ unknowns in the form $A\textbf{x}=\textbf{b}$ where $\textbf{x}$ is all of the $u^{n+1}$ values, $\textbf{b}$ is the explicit side, and $A$ is the coefficients from the left hand side.
Example problem
For example we will use the same physical problem as in part 2 (the only difference is the length scale). A $1x1$ flat plate has a thermal diffusivity of $\alpha=.001$. The temperature is fixed at $u=1$ on an inner circular boundary and is fixed at 0 on four outer boundaries. Elsewhere, the initial temperature is $u=0$. Find the temperature distribution over time.
Meshing
Much of the best meshing software is propietary and expensive, but there are some good free programs like Gmsh. We will implement code to read in and use a *.msh file.
We will test out the mesh below. It has $1,992$ nodes.
The code
Now let’s lay out the code. We are going to break it up into three steps: initialize relevant physical parameters, import the mesh, set the boundary conditions, assemble the coefficient matrix, and set up the time loop.
Step 1: Initialize physical parameters
%Physical Quantities nts=100; ntsabout=100; dt=.03; alpha=.001; c=alpha*dt/2;
Step 2: Import the Mesh
[xyz,mesh,nn,tri,bnd,map]=importmesh2('circle_fine.msh');
The function will return
- xyz: the nodes in a (nn,2) where nn is the number of points in the mesh.
- mesh: A structure array containing the fields nbr (neighboring points), dx and dy (the distances to respective points), coeff the coefficients of the derivative approximation, and bnd, the boundary type of the point.
- tri: the “connectivity of the mesh (for visualizations).
- nn: The number of nodes in the mesh
- bnd: a list of the nodes in the boundary. Only necessary for an implicit formulation.
- map: The points in the mesh not on a boundary.
I will not include the importmesh2 code in this post but you can access the text here.
Step 3: Apply Initial and Boundary Conditions
%Initialize arrays
T = zeros(nn,1); A=zeros(nn); b=zeros(nn,1);
%Initial conditions
for n=bnd
if mesh(n).bnd==5
T(n)=1;
end
end
Step 4: Assemble coefficient matrix and boundary contribution to the rhs vector
for i=bnd
A(i,i)=1;
end
for i=map
A(i,i)=1+c*mesh(i).coeff(end);
for j = 1:length(mesh(i).nbr)
A(i,mesh(i).nbr(j))= -c*mesh(i).coeff(j);
end
end
b(bnd)=T(bnd);
Step 5: Time Loop
for t=1:nts
%update rhs
for n=map
dd=mesh(n).coeff*[T(mesh(n).nbr); -T(n)];
b(n)=c*dd+T(n);
end
%solve matrix equation
%T=Ai*b; %use inverse of A, requires Ai=inv(A)
%T=A\b; %MATLAB built in mldivide
%T=L\T; %T=U\T; %LU decomposition, requires [L,U]=lu(A);
[T,flag]=gmres(A,b); %GMRES method
%update visualization
if mod(t,ntsabout)==0
trisurf(tri,xyz(:,1),xyz(:,2),T,'FaceColor','interp','EdgeColor', 'none')
axis([0,1,0,1]); view(0,90); colorbar; grid off;
outframe(t) = getframe;
end
end %time loop
Results
We already showed a visualization at the top of the post so let's look at run-time comparison of explicit and a few different matrix solver methods with implicit. The methods are explicit (FTCS), MATLAB’s mldivide (\), $LU$ decomposition with back-substitution, inverting $A$, and the GMRES method. We used the mesh shown above and a refined mesh with four times as many nodes. We calculated two time lengths, $3~\mathrm{s}$ and $30~\mathrm{s}$. Computation times are given in seconds.
| Method | $t=3~\mathrm{s}$ (coarse) | $t=30~\mathrm{s}$ (coarse) | $t=3~\mathrm{s}$ (fine) | $t=30~\mathrm{s}$ (fine) |
|---|---|---|---|---|
| Explicit | 11.94 | 121.30 | N/a | N/a |
| A\b | 42.28 | 411.5 | N/a | N/a |
| LU | 2.50 | 25.04 | 35.35 | 184.5 |
| Inversion | 1.72 | 17.08 | 67.42 | 146.8 |
| GMRES | 2.76 | 24.18 | 29.71 | 225.3 |
Since the coefficient matrix doesn’t change with every time step, the speed during the time loop is greatly increased by inverting $A$ or determining its $LU$ decomposition beforehand. The GMRES method on the other hand, is fast because it is designed to handle sparse matrices like $A$.
We are only able to get away with inverting $A$ because our mesh is very small. Matrix inversion is a computationally expensive operation that does not scale well (see here). For example, if one quadruples the mesh points as we have, the run time for inverting $A$ theoretically increases by a factor of 64. Furthermore MATLAB documentation recommends against using the inv command whenever possible. The $LU$ decomposition is generally considered to be better practice than inversion, but it also scales poorly for large matrices unless an algorithm that takes advantage of the sparse nature of $A$ is employed.
In a reasonably large computation, GMRES would generally be the best method unless another method can be employed that efficiently inverts sparse matrices (such methods exist for specialized problems).
Structured, transformation-free finite differences on complex geometries
Posted on January 22, 2014
Introduction
Objective: Obtain a numerical solution for the 2D Heat Equation on mesh with circular boundaries in MATLAB using an explicit finite difference formulation with Richardson extrapolation (and without coordinate transformation).
Helpful background: A basic understanding of PDEs (partial differential equations), MATLAB coding (for loops, arrays, functions, maps, trisurf, and bitget), basic derivative approximations with finite differences and Richardson extrapolation.
Modeling the problem
First let’s introduce the heat equation. The heat equation in two dimensions is $$u_t=\alpha(u_{xx}+u_{yy})$$ where $u(x,y,t)$ is a function describing temperature and $\alpha$ is thermal diffusivity.
Numerically discretizing the equations We are going to solve the heat equation numerically with an explicit formulation. We talk about this a little in our previous post on the heat equation. There are many methods that solve this, but the simplest is an explicit finite difference formulation. The major difference here is how we handle the more difficult geometry of a circular disk. If none of the points neighbor the boundary, we will use the central difference approximation for our second derivatives. The approximations for $u_{xx}$ and $u_{yy}$ are \begin{eqnarray} u_{xx}(i,j)=\displaystyle\frac{u(i+1,j)-2\cdot u(i,j)+u(i-1,j)}{(\Delta x)^2} \\ u_{yy}(i,j)=\displaystyle\frac{u(i,j+1)-2\cdot u(i,j)+u(i,j-1)}{(\Delta y)^2}. \end{eqnarray}
Calculating the second derivatives for points near boundaries with curvature will be covered in the next two sections.
We will then update the temperature using a first derivative forwards in time. $$ u_t^n=\frac{u^{n+1}-u^n}{\Delta t}.$$ The final formulation is then \begin{eqnarray} u^{n+1}(i,j) &=& u^n(i,j)+\alpha\cdot \Delta t\cdot \left(u_{xx}^n(i,j)+u_{yy}^n(i,j)\right) \end{eqnarray}
Geometries with Curvature When geometries become more complex than a 1D problem on a line or a 2D cartesian grid, many numerical analysts move on to one of three methods: finite volume methods, finite element methods, or finite difference methods with coordinate transformations. These formulations are much more difficult to implement, but can essentially handle any geometry (with varying difficulty).
Instead of using one of these methods we will stick with finite differences and take advantage of a tool call Richardson extrapolation to keep the second order accuracy that led to a nice solution in Part 1.
Let’s set up a specific example. A $4x4$ flat plate has a thermal diffusivity of $\alpha=.01$. The temperature is fixed at $u=1$ in an inner circle with radius $1$. Elsewhere, the initial temperature is $u=0$ and the outer boundaries are fixed at $u=0$ for all time. Find the temperature distribution over time.
(Note: I left off any units and have some simplified numbers for temperature and plate dimensions. Feel free to change them as you please, but make sure your formulation is still stable.)
The initial condition would look something like this:
Richardson Extrapolation Before we get started, it may help to glance at some of the basics of Richardson Extrapolation at Wikipedia.
The biggest challenge in our problem is that it requires a second derivative, which proves to be a little harder to compute with second order spatial accuracy. First and foremost, we can’t do it with just the two neighboring points (like we would be able to with evenly spaced points); we will need to use one more. Consider the points below. Assume that at each point $1,2,3,4$ we know the value of a function $f$ are $f_1,f_2,f_3,f_4$.
We will use information at the points $1,2,3,$ and $4$ to approximate the second derivative at point $3$, $f_3^{\prime\prime}$ . Why point $3$? In our particular problem, the second derivatives at points $1$ and $2$ can be approximated with a standard central difference and point $4$ will be a boundary, so the second derivative will not need to be calculated there.
Our first step will be to calculate the first derivatives at points $2,3,$ and $4$. These are fairly straightforward; we will use a central difference at point $2$ and Richardson extrapolation and points 3 and 4. They should look something like this \begin{eqnarray} f_2^{\prime} &=& \displaystyle\frac{f_3-f_1}{2\cdot \Delta x_1} \\ f_3^{\prime} &=& \displaystyle\frac{k_1\cdot (f_4-f_3)}{(k_1+1)\cdot \Delta x_2}+\frac{(f_3-f_2)}{(k_1+1)\cdot\Delta x_1} \\ f_4^{\prime} &=& \displaystyle\frac{k_2\cdot (f_4-f_3)}{(k_2-1)\cdot\Delta x_2}-\frac{f_4-f_2}{(k_2-1)\cdot (\Delta x_1+\Delta x_2) } \end{eqnarray} Where $k_1= \frac{ \Delta x_1}{ \Delta x_2}$ and $k_2=\frac{ \Delta x_1+ \Delta x_2}{ \Delta x_2}$ . Now we will use these to approximate the second derivative at $x_3$ with Richardson extrapolation. This is very similar to the formula except we will use a different value of $k$, namely $k_3=\frac{4\cdot k_1-1}{2\cdot k_1-2}$.
After wading through the algebra, your expression will simplify to $$f_3^{\prime\prime} = \frac{\Delta x_2^3\cdot (f_1-2 f_2+f_3)+\Delta x_1^3\cdot (6 f_4-6 f_3)+\Delta x_1^2\cdot \Delta x_2\cdot (-f_1+8 f_2-7 f_3)}{\Delta x_1^2\cdot \Delta x_2\cdot (\Delta x_1+\Delta x_2)\cdot (2 \Delta x_1+\Delta x_2)} $$
This is a pretty costly formula compared to the central difference method. Fortunately, we will not have to use this equation very often; only when the points are neighboring the boundary. Meanwhile, this allows us to use the cheap and effective central difference method at all other points. Therefore the overall computation should be fairly inexpensive.
We will also need to generate a mesh. Below is an example of the mesh. The elements have been triangulated for simple viewing in MATLAB, but there is no triangulation and no element formulation in the solution.
The original mesh here was a $22x22$ grid, but there were an additional 40 points added on the boundary to maintain the curvature of the circle. The important part is finding the $\Delta x_2$ and $\Delta y_2$ values for each of the points immediately neighboring a boundary and creating an additional point on the mesh.
When we loop through the mesh points we will ignore all points where the temperature is specified, use Richardson Extrapolation on the points adjacent to the 40 added points, and uses central differences elsewhere.
A Quick Look at Stability In the previous part we discussed stability, namely that in order for the old formulation to hold we needed to satisfy $$ \Delta t < \frac{\Delta x_1^2}{4\alpha}.$$ We will not perform a proper stability analysis, but our empirical results show that $$ \Delta t < \frac{\Delta x_1\cdot min(\Delta x_2)}{4\alpha}$$ is generally sufficient. Once you have your code written it is easy to empirically test different values of $\Delta t$.
The code
We are going to break it up into five steps: Create the Richardson extrapolation function, initialize relevant physical values, generate the mesh, set the boundary conditions, and set up the time loop. The time loop will consist of calculating the derivatives at each point, updating the temperature for each point, and then updating the visualization.
Step 1 Richardson Extrapolation
function [ddf3a] = richardson(dx1,dx2,f1,f2,f3,f4)
ddf3a = (dx2^3*(f1-2*f2+f3) + ...
dx1^3*(6*f4-6*f3) + ...
dx1^2*dx2*(-f1+8*f2-7*f3))...
/(dx1^2*dx2*(dx1+dx2)*(2*dx1+dx2));
end
Step 2 Initialize variables
%Initialize Physical Values dt=.01; %time step nts=500; %number of time steps alpha=.01; %thermal diffusivity bounds=[-2 2 -2 2]; %corners of outer domain %Mesh Variables nx=50; ny=50; %number of points in the x and y directions %distance in between points dx1=(bounds(2)-bounds(1))/(nx-1); dy1=(bounds(4)-bounds(3))/(ny-1);
Step 3 Generate the Mesh
[xyz,skip,dx2,dy2,tri]=genmesh(bounds,nx,ny); %The derivatives and temperature will be stored in a 1D arrays nodes=length(skip); uxx=zeros(nodes,1); uyy=zeros(nodes,1); T=zeros(nodes,1);
The function will return
- xyz: the nodes in a (np,2) where np is the number of points in the mesh.
- skip: an array that shows whether a point is on a boundary or neighboring one.
- dx2 and dy2: maps relating the distance from a point to the boundary if it neighbors the boundary.
- tri the “connectivity" of the mesh.
An alternative to creating your own tri connectivity would be using the MATLAB built in function tri=delaunay(x,y) but it will not look as good as if you make it yourself.
I will not include any of the code in this post (my version is 160 lines long and it is mostly boring) but you can access the text here.
Step 4 Apply Initial and Boundary Conditions
for p=1:length(skip)
if skip(p) < 0
u(p)=1.0;
else
u(p)=0.0;
end
end
Step 5 Time Loop The time loops has three components, first calculate the second derivatives, then update temperature, then update the visualization.
One note before we get into the code. We are using the MATLAB function “bitget” which determines based of the values of skip(p) (see Step 3) whether it is close to the boundary. This is by all means not necessarily the best way to determine whether a point neighbors a boundary, but it works and is not too costly.
for t=1:nts
for i=2:ny-1
for j=2:nx-1
p=nx*(i-1)+j;
if skip(p) < 0
continue
end
if bitget(skip(p),1)==1
uxx(p)=richardson(dx1,abs(dx2(p)),u(p-2),u(p-1),u(p),T_b);
elseif bitget(skip(p),3)==1
uxx(p)=richardson(dx1,abs(dx2(p)),u(p+2),u(p+1),u(p),T_b);
else
uxx(p)=(u(p-1)-2*u(p)+u(p+1))/dx1^2;
end
if bitget(skip(p),2)==1
uyy(p)=richardson(dy1,abs(dy2(p)),u(p-2*nx),u(p-nx),u(p),T_b);
elseif bitget(skip(p),4)==1
uyy(p)=richardson(dy1,abs(dy2(p)),u(p+2*nx),u(p+nx),u(p),T_b);
else
uyy(p)=(u(p-nx)-2*u(p)+u(p+nx))/dy1^2;
end
end
end
for i=2:nx-1
for j=2:ny-1
p=nx*(i-1)+j;
if skip(p)<0
continue
end
u(p)=u(p)+alpha*dt*(uxx(p)+uyy(p));
end
end
trisurf(tri,xyz(:,1),xyz(:,2),u,'FaceColor','interp');
frame = getframe(1);
end
Results
Below are two animations of the temperature distribution over time.
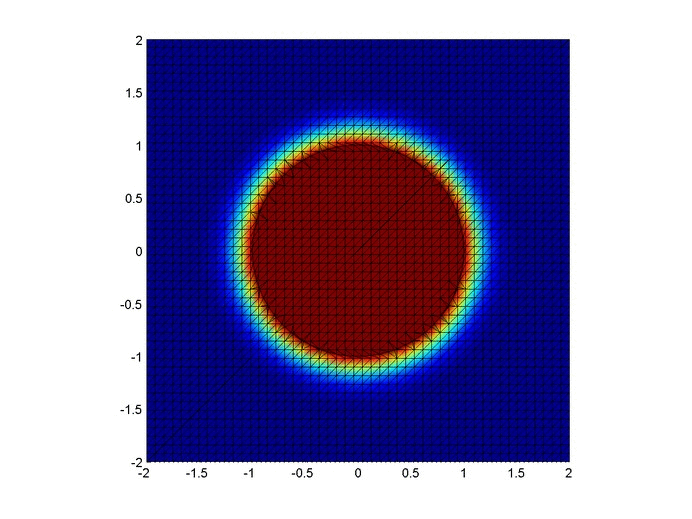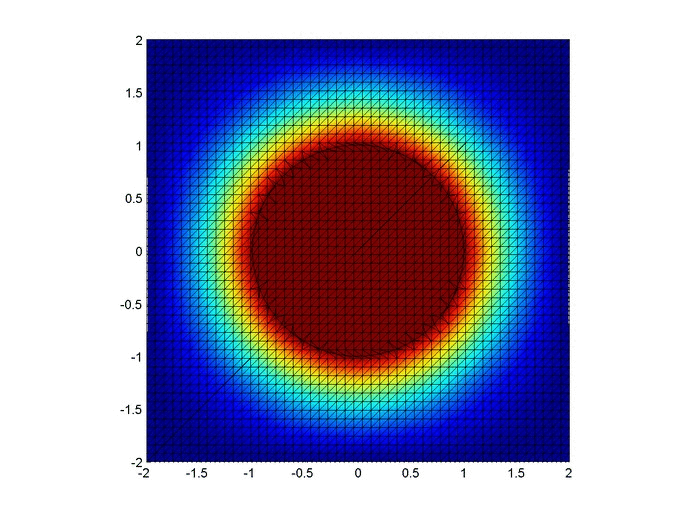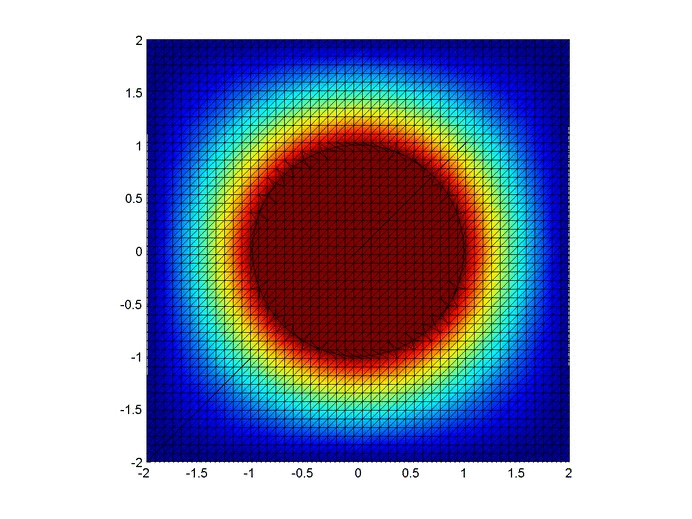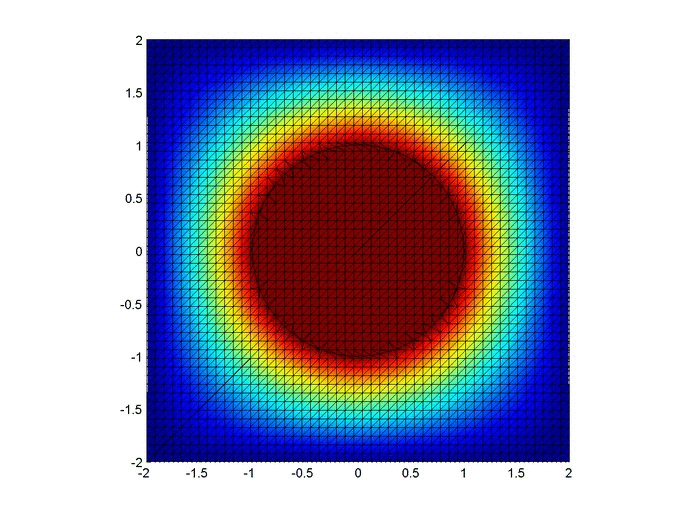

Some notes about the code
If you are a novice programmer, you may not have heard of maps. Maps are "objects with keys that index to values" (see here and here). They are similar to an array, except that keys must be unique, keys don't need to be integers, and key values typically aren't ordered. A map is by no means necessary here, but it is an efficient way to store and quickly retrieve the $\Delta x_2$ and $\Delta y_2$ values.
The most confusing part of the code above is implementation of the skip array with bitget. Basically, skip is an array with an integer for every node.
- If a node p is on or inside the circle, skip(p)=-1.
- If it is outside the circle and not adjacent to it, skip(p)=0.
- If it is adjacent to the circle (left, below, right, above) then we add 1,2,4,8 respectively to skip(p). For example, if a point is below and to the right of points on the circle, then skip(p)=6.
We can then reverse engineer skip(p) with bitget. This is not necessarily the best or only way, but it is a relatively simple implementation.
You can save some space in memory by letting uxx and uyy be single values instead of arrays. This however, would either require two arrays for temperature (an old and a new) or some algorithm to keep from overwriting old values of temperature before all derivatives are calculated. Since we are dealing with a relatively coarse 2D mesh, this is not a significant issue.
Finite Difference Solution of the Heat Equation on a Structured Mesh
Posted on November 19, 2013
Introduction
In this post we will numerically solve the heat equation with an explicit finite difference formulation.
Objective: Obtain a numerical solution for the 2D Heat Equation in MATLAB using an explicit finite difference formulation.
Helpful background: basic understanding of PDEs (partial differential equations), basic MATLAB coding (for loops and arrays), and basic derivative approximations with finite differences.
Modeling the problem
First let’s introduce the heat equation. The heat equation in two dimensions is $$u_t=\alpha(u_{xx}+u_{yy})$$ where $u(x,y,t)$ is a function describing temperature and $\alpha$ is thermal diffusivity.
Numerically discretizing the equations We are going to solve the heat equation numerically. There are many methods that solve this, but the simplest is an explicit finite difference formulation. Explicit means the solution at a certain time step depends only on previous step, as opposed to implicit (see here) where the solution depends on next time step. Finite differences are a simple way to use neighboring grid points to approximate derivatives.
We will use the central difference approximation for our second derivatives. The approximations for $u_{xx}$ and $u_{yy}$ are \begin{eqnarray} u_{xx}(i,j)&=&\displaystyle\frac{u(i+1,j)-2\cdot u(i,j)+u(i-1,j)}{(\Delta x)^2} \\ u_{yy}(i,j)&=&\displaystyle\frac{u(i,j+1)-2\cdot u(i,j)+u(i,j-1)}{(\Delta y)^2}. \end{eqnarray} These are all at time $n$ (they are not exponents). We will use the forward difference approximation for $u_t$. We have
$$ u_t^n=\frac{u^{n+1}-u^n}{\Delta t}.$$
This is for every point $(i,j)$. Now we can take these 3 expressions, combine them, and solve for $u^{n+1}$.
\begin{eqnarray} u_t^n(i,j) &=& \alpha(u_{xx}^n(i,j)+u_{yy}^n(i,j)) \\ \frac{u^{n+1}(i,j)-u^n(i,j)}{\Delta t} &=& \alpha\left[\frac{u(i+1,j)-2\cdot u(i,j)+u(i-1,j)}{(\Delta x)^2}+ \frac{u(i,j+1)-2\cdot u(i,j)+u(i,j-1)}{(\Delta y)^2}\right] \\ u^{n+1}(i,j) &=& u^n(i,j)+\alpha\cdot dt\left[ \frac{u(i+1,j)-2\cdot u(i,j)+u(i-1,j)}{(\Delta x)^2}+\frac{(u(i,j+1)-2\cdot u(i,j)+u(i,j-1)}{(\Delta y)^2}\right] \end{eqnarray}
A quick look at stability The formulation we used (forward in time, centered in space) is only conditionally stable. We can show (but won’t here) with Von Neumann Stability Analysis, that we need the discretized time step $\Delta t$ to satisfy $$ \Delta t< \frac{\Delta x^2}{4\alpha}.$$Once you have your code written it is easy to empirically test this.
The code
Let’s set up a specific example. A $1x1$ flat plate has a thermal diffusivity of $\alpha=.01$. The temperature is fixed at $u=1$ on the top and right edges and $u=0$ on the bottom and left edges. Elsewhere, the initial temperature is $u=0$. Find the temperature distribution over time.
(Note: I left off any units and have some simplified numbers for temperature and plate dimensions. Feel free to change them as you please, but make sure your formulation is still stable.)
Now let’s lay out the code. We are going to break it up into three steps: Initialize relevant physical values, set the boundary conditions, and set up the time loop. The time loop will consist of calculating the derivatives at each point, updating the temperature for each point, and then updating the visualization.
Step 1: Initialize variables We will start by initializing relevant physics variables for the time step size, number of time steps, thermal diffusivity, reference plate length, number of points in the x and y direction, and the spatial discretization $\Delta x$ and $\Delta y$.
You can also preallocate the matrices for $u$, $u_{xx}$, and $u_{yy}$.
%Initialize Variables dt=.005; %time step nts=500; %number of time steps alpha=.01; %thermal diffusivity l=1; %reference length plate nx=50; ny=50; %number of points in the x and y directions dx=l/(nx-1); dy=l/(ny-1); %discretized distance in between points %Temperature and the derivatives will be stored in a two dimensional array u = zeros(nx,ny); uxx = zeros(nx,ny); uyy = zeros(nx,ny);
Step 2: Apply Initial and Boundary Conditions
%Initial/Boundary Conditions for i=1:ny u(1,i)=1; end for i=1:nx-1 u(i,ny)=1; end
Step 3: Time Loop Here is the meat of the code. The time loops has three components, first calculate the second derivatives, then update temperature, then update the visualization.
for t=1:nts
%Calc the Spatial 2nd Derivative, Centered in Space
for i=2:nx-1
for j=2:ny-1
uxx(i,j)=(u(i+1,j)-2*u(i,j)+u(i-1,j))/(dx)^2;
uyy(i,j)=(u(i,j+1)-2*u(i,j)+u(i,j-1))/(dy)^2;
end
end
%Update Temperature, Forwards in Time
for i=2:nx-1
for j=2:ny-1
u(i,j)=u(i,j)+alpha*(uxx(i,j)+uyy(i,j))*dt;
end
end
%Visualization
contourf(u)
axis equal
M(t) = getframe;
end %time loop
Results
Below are 2 GIFs (one is a contour plot, the other is a surface plot) of the temperature distribution over time.
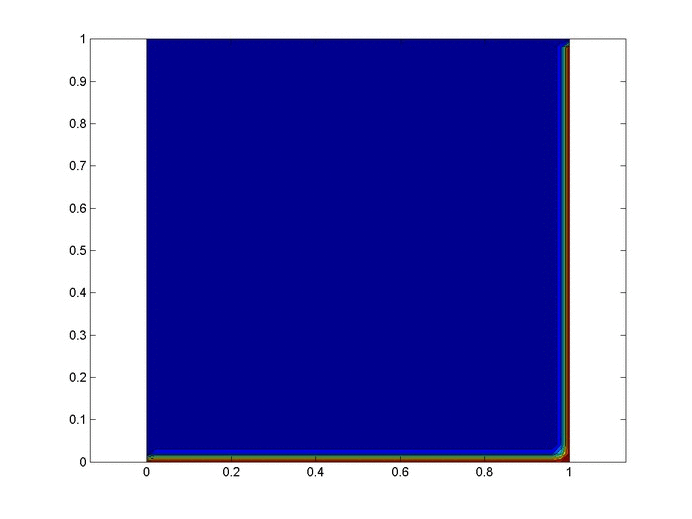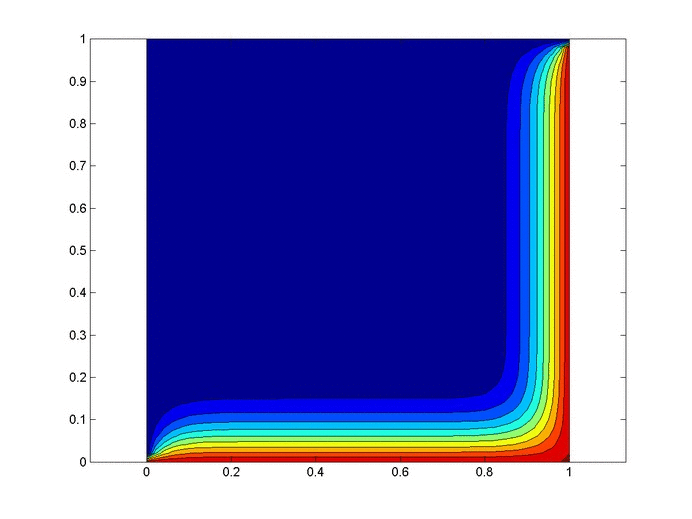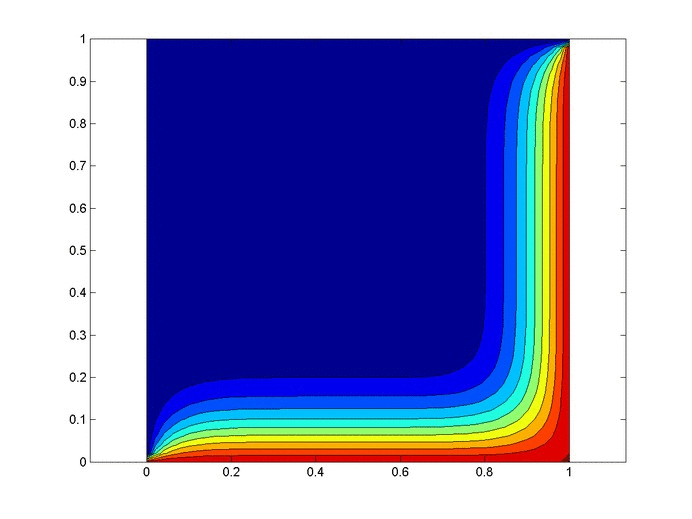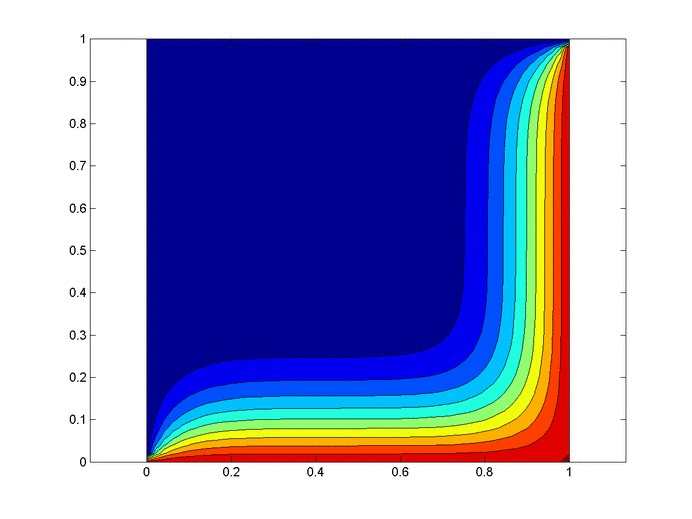
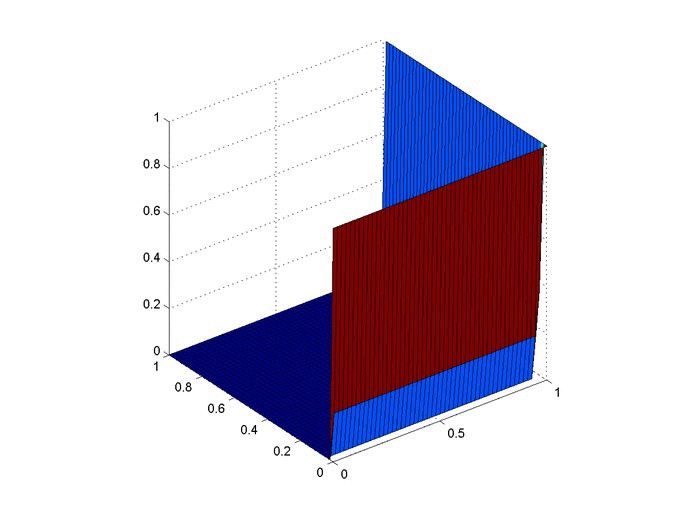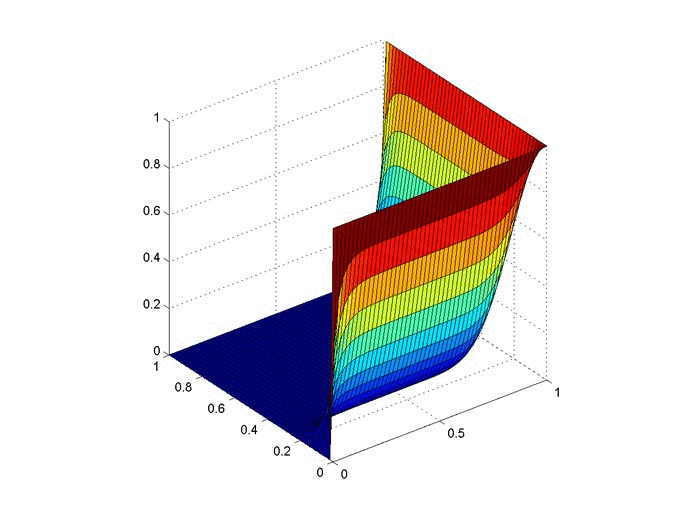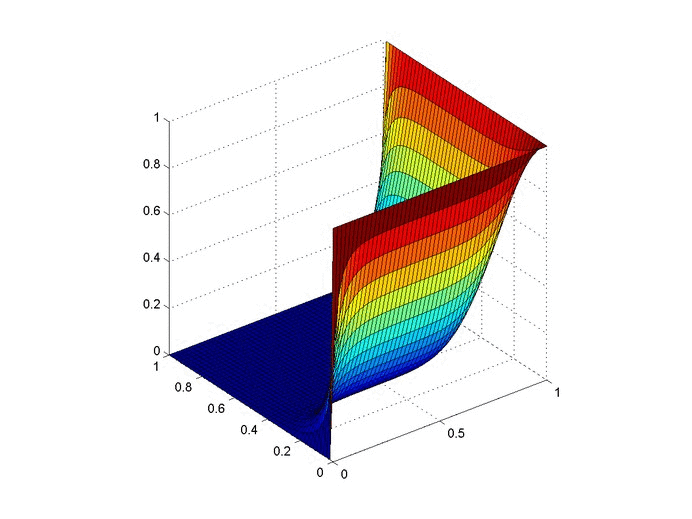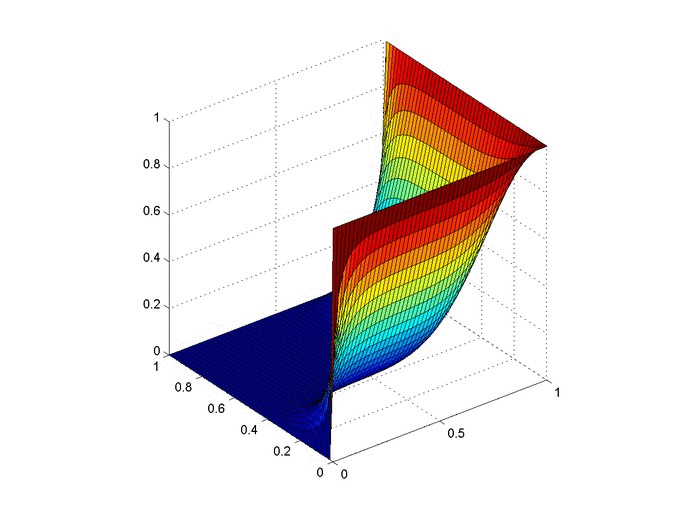
Projectile Motion with (Quadratic) Drag
Posted on October 31, 2013
Projectile motion is discussed and worked out in nearly every college physics, calculus, and dynamics class, but examples always seem to neglect or over-simplify drag. In this post we will tackle an analytic solution that models drag for a falling object.
Let’s suppose we are dropping a ball from a height \(h_0\) with a velocity \(v_0\). In a vaccuum, the only force is gravity, $mg$. Then projectile motion without drag begins with Newton’s second law $$F_{net}=mg=ma \rightarrow a=g.$$ Acceleration can then be twice integrated with respect to time, yielding $$p(t)=\frac{g}{2}t^2+v_0t+h_0.$$ Given a constant force (i.e. not dependent on time or velocity) this is a simple integration with respect to time and the math is rather elementary. We can make it much more challenging by inserting an additional force term, drag, which is dependent on velocity: $$F=mg-D =ma \rightarrow a=g-D/m.$$ Many approximations for drag can be applied, but the most accurate model is $$D=1/2 \rho v^2\cdot c_d\cdot A.$$ Here \(c_d\) is coefficient of drag (dimensionless), A is the cross-sectional area, and \(\rho\) is the density of the medium the object is falling (e.g. air is $1.225 ~ \mathrm{kg}/\mathrm{m}^3$). Let’s jump into the math. $$a=g-D/m=g-\frac{\rho\cdot c_d\cdot A}{2m}v^2.$$ Now let \(a=dv/dt\) and for simplicity let \(k^2=\frac{\rho\cdot c_d\cdot A}{2mg}\). Coincidentally, $\frac{1}{k}$ is also the terminal velocity of a falling object. We have \begin{eqnarray} \frac{dv}{dt} &=& g-gk^2 v^2 \\ g\cdot dt &=& \frac{dv}{1-k^2 v^2}. \end{eqnarray} In its current form, this is not a simple integration. It can be evaluated with the hyperbolic arc-tangent, but to keep the equations in terms of more recognizable functions we will instead apply a partial fraction expansion $$\frac{dv}{1-k^2 v^2}=\frac{1}{2k}\left[\frac{dv}{v-1/k}-\frac{dv}{v+1/k}\right].$$
If this is confusing, you can review partial fraction expansions here
Now we can integrate \begin{eqnarray} g\cdot dt &=& \frac{1}{2k} \left[\frac{dv}{v+1/k}-\frac{dv}{v-1/k}\right]. \\ g\cdot t &=& \frac{1}{2k} \left[\ln(v+1/k)-\ln(v-1/k)\right]+C_1. \end{eqnarray}
We now have time as a function of velocity, but that isn’t very useful. Let’s see if we can solve for $v$: \begin{eqnarray} g\cdot t &=& \frac{1}{2k} \left[ \ln(v+1/k)-\ln(v-1/k) \right] +C_1 \\ g\cdot t &=& \frac{1}{2k}\cdot\ln\left[\frac{v+1/k}{v-1/k}\right]+C_1 \\ 2gk\cdot t+C_2 &=& \ln\left[\frac{v+1/k}{v-1/k}\right]\\ \end{eqnarray}
Now we can exponentiate both sides
\begin{eqnarray} Ce^{2gk\cdot t}=\frac{v+1/k}{v-1/k}=\frac{2/k}{v-1/k}+1. \\ \end{eqnarray} Now we can solve for $v$. \begin{eqnarray} v &=& \frac{2/k}{Ce^{2gk\cdot t}-1}+1/k. \\ &=& \frac{1}{k}\left(\frac{2}{Ce^{2gk\cdot t}-1}+1\right). \\ \end{eqnarray} Now we eliminate that pesky \(C\) by applying an initial condition for velocity. We are simply dropping something so let \(v(0)=0\).
We have \begin{eqnarray} v &=& \frac{1}{k}\left(\frac{2}{Ce^{2gk\cdot 0}-1}+1 \right) \\ &=& \frac{1}{k}\left(\frac{2}{C-1}+1 \right) \rightarrow C=-1. \end{eqnarray} Therefore $$v = \frac{1}{k}\left(1-\frac{2}{e^{2gk\cdot t}+1}\right).$$ Velocity is all fine and dandy, but what we are really after is position. This requires one more integration, but fortunately it’s a little simpler: This takes a little rewriting u-substitution. We have \begin{eqnarray} \frac{dp}{dt} &=& \frac{1}{k}\left(1-\frac{2}{e^{2gk\cdot t}+1}\right) \\ &=& \frac{1}{k}\left(1-\frac{2e^{2gk\cdot t}+2}{e^{2gk\cdot t}+1}+\frac{2e^{2gk\cdot t}}{e^{2gk\cdot t}+1}\right) \\ &=& \frac{1}{k}\left(1-2+\frac{2e^{2gk\cdot t}}{e^{2gk\cdot t}+1}\right). \end{eqnarray}
Now this is in a form where we can intuitively apply $u$-substitution. We have \begin{eqnarray} p=\frac{1}{gk^2}\ln[e^{2gk\cdot t}+1]-\frac{t}{k}+C. \end{eqnarray} Now if we apply the initial condition \(h(0)=h_0\) we have \begin{eqnarray} p &=& \frac{1}{gk^2} \ln\left[e^{2gk\cdot t}+1\right]-\frac{\ln(2)}{gk^2}-\frac{t}{k}+h_0. \\ &=& \frac{1}{gk^2} \ln\left[\frac{e^{2gk\cdot t}+1}{2}\right]-\frac{t}{k}+h_0. \end{eqnarray}
Let's put this to use with a quick example. Let's say we are dropping two balls off a tower $56~\mathrm{m}$ tower. They have the same cross-sectional area $A=1/3 ~ \mathrm{m}^2$ and drag coefficient $c_d=0.5$, but have different masses of $1 ~ \mathrm{kg}$ and $5 ~ \mathrm{kg}$. We can use the above formula to find how long it takes them to hit the ground.
Clearly accounting for drag is important if the object falling is very light, very large, or is falling through a medium with a high density.