Winning Lotería and Countdown
Posted on June 2, 2019
Updated on June 4, 2019
I made a few changes from the original post. I misread allowable order of operations (the equivalent of "parentheses are ok", which drastically increases solvable numbers). I decided to leave it in as an interesting twist on the problem.
I also left out the case of six small numbers (another misread), which I have since added.
Below are solutions to the Classic and Express problems posed on May 31's edition of the Riddler on fivethirtyeight.com, "Can You Win The Lotería?".
Riddler Express - Lotería
First, a brief solution to the Riddler Express. The question posed is: for $N=54$ total images, and $n=16$ images per player card, how often will the game end with one empty card of images?
Two things must be considered: how often do the two players have unique cards (a necessary condition), and if that is met, how often will an entire card be filled before any images on the second card are filled?
We must first consider the necessary condition that the players have unique images on their cards. It helps to think about image "selection" successively. The first player can pick their entire card without concern. Then the second player "picks" their images for the second card one by one. For $N=54$ and $n=16$, there are $54$ options, $54-16=38$ of which are favorable, so probability the first image for the second card is not on the first card is $\frac{38}{54}$. The second image cannot be the first (and will not be the previous image), so there are now $53$ options, $37$ of which are favorable, yielding a probability of $\frac{37}{53}$. Continuing this logic, the probability the cards are unique is
$$ \frac{38}{54}\cdot\frac{37}{53}\cdot\frac{36}{52}\cdot...\cdot\frac{23}{39} \approx 0.001054.$$In general, the probability can be written as
$$ \displaystyle\frac{\binom{N-n}{n}}{\binom{N}{n}}.$$ Second, assuming the two cards are unique, how often will you win before the other player crosses a single image off their card? The extraneous cards are meaningless, akin to burn cards. WLOG, if you have images $1$-$16$, your opponent has $17$-$32$, then the favorable outcomes are all $16!$ arrangements of your cards, followed by all $16!$ arrangements of your opponents outcomes. The total number of arrangements is $32!$, the arrangements of all cards. The probability is then $$ \displaystyle\frac{16!\cdot 16!}{32!} \approx 1.664\times 10^{-9}. $$In general, the probability can be written as
$$ \displaystyle\frac{(n!)^2}{(2n)!}. $$Note, there is no $N$ term in this expression. The simulation in the code below considers all $N$ cards to verify its invariance.
from ncr import ncr #n choose r
import numpy as np
def you_win(photo_order, n):
"""WLOG you have photos 0 to n-1, opponent has n to 2n-1
Check if all of your photos appear before any of your opponents"""
n_count = 0
for i in photo_order:
if i < n:
n_count += 1
if n <= i < 2*n:
return False
if n_count == n:
return True
def main():
N = 54 # Total number of photos
n = 16 # Number of photos per player
num_sim = 10000 # Number of simulations
# Simulate Unique
count = 0
for _ in xrange(num_sim):
list_1 = np.random.choice(N, n, replace=False) # Your photos
list_2 = np.random.choice(N, n, replace=False) # Opponent's photos
if set(list_1) & set(list_2): # Check for intersection
count += 1
print "probability unique:", \
ncr(N-n, n) / float(ncr(N, n)), \
1.0 - count / float(num_sim)
# Simulate You Win
count = 0
for _ in xrange(num_sim):
photo_order = np.arange(N)
np.random.shuffle(photo_order)
if you_win(photo_order, n):
count += 1
print "probability you win:", 1./ncr(2 * n, n), count / float(num_sim)
if __name__ == "__main__":
main()
Riddler Classic - Countdown
$\newcommand{\Lone}{\mathrm{L}_{1}}$ $\newcommand{\Ltwo}{\mathrm{L}_{2}}$ $\newcommand{\Lthree}{\mathrm{L}_{3}}$ $\newcommand{\Lfour}{\mathrm{L}_{4}}$ $\newcommand{\a}{\mathrm{a}}$ $\newcommand{\b}{\mathrm{b}}$ $\newcommand{\c}{\mathrm{c}}$ $\newcommand{\d}{\mathrm{d}}$ $\newcommand{\e}{\mathrm{e}}$The remainder of this post will focus on the countdown problem, namely a brute force approach to counting all possible outcomes in a reasonable amount of time, follwed by a discussion of results. See code here.
The most fruitful combination is shown to be $5$, $6$, $8$, $9$, $75$, $100$, which yields $691$ different three-digit numbers. The least fruitful is shown to be $1$, $1$, $2$, $2$, $3$, $25$, which yields only $20$ different three-digit numbers.
Statistics for the various strategies (selecting 1 through 4 large numbers) are summarized, and it is shown that selecting two large numbers is the most advantageous, followed closely by selecting three large numbers.
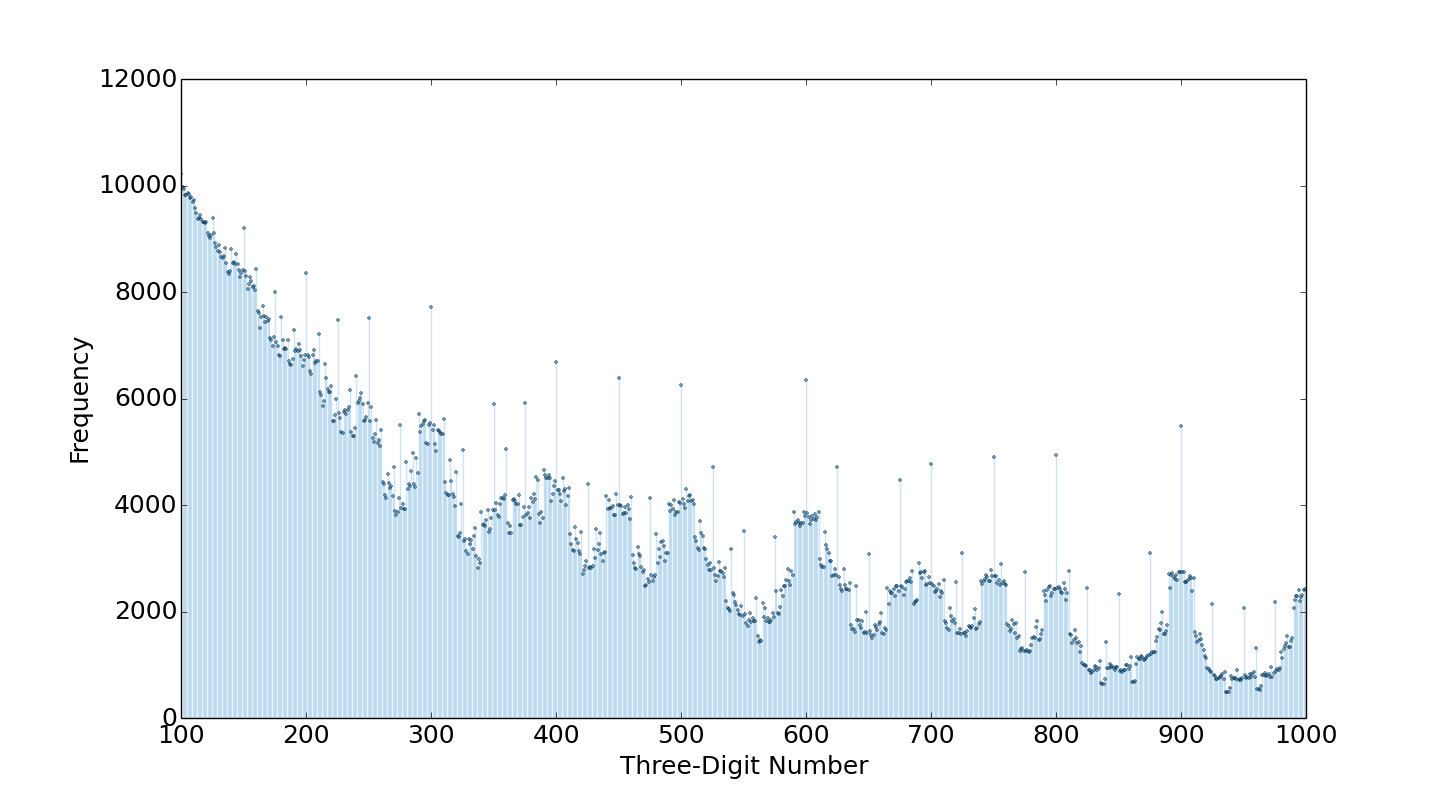
Finally, a histogram of the three-digit numbers frequency among the $10,603$ combinations shows what is intuitive, at least in hindsight: smaller three-digit numbers, and multiples of $25$, $50$, and especially $100$ are the most common.
Generating Combinations
First we must consider all possible combinations of the small and large numbers. We will denote large numbers with $\Lone$, $\Ltwo$, $\Lthree$, and $\Lfour$ and small numbers with $\a$, $\b$, $\c$, $\d$ and $\e$. A player can selected between zero and four large numbers, and the small numbers may repeat once. There are $11$ possible scenarios, divided by double lines in the table below by strategy.
| Pattern | Number of Combinations |
|---|---|
| $\a\b\c\d\e\mathrm{f}$ | $\binom{10}{6}$ |
| $\Lone\a\a\b\b\c$ | $\binom{4}{1}\cdot\binom{10}{2}\cdot\binom{8}{1}$ |
| $\Lone\a\a\b\c\d$ | $\binom{4}{1}\cdot\binom{10}{1}\cdot\binom{9}{3}$ |
| $\Lone\a\b\c\d\e$ | $\binom{4}{1}\cdot\binom{10}{5}$ |
| $\Lone\Ltwo\a\a\b\b$ | $\binom{4}{2}\cdot\binom{10}{2}$ |
| $\Lone\Ltwo\a\a\b\c$ | $\binom{4}{2}\cdot\binom{10}{2}\cdot\binom{8}{1}$ |
| $\Lone\Ltwo\a\b\c\d$ | $\binom{4}{2}\cdot\binom{10}{4}$ |
| $\Lone\Ltwo\Lthree\a\a\b$ | $\binom{4}{3}\cdot \binom{10}{1}\cdot \binom{9}{1}$ |
| $\Lone\Ltwo\Lthree\a\b\c$ | $\binom{4}{3}\cdot\binom{10}{3}$ |
| $\Lone\Ltwo\Lthree\Lfour\a\a$ | $\binom{4}{4}\cdot\binom{10}{1}$ |
| $\Lone\Ltwo\Lthree\Lfour\a\b$ | $\binom{4}{4}\cdot\binom{10}{2}$ |
Generating Permutations
These can be generated individually with the help of the Python itertools library. As a sample, consider $\Lone\Ltwo\a\a\b\c$.
import itertools
L_array = [25., 50., 75., 100.]
s_array = [float(i) for i in range(1, 11)]
for s in itertools.combinations(s_array, 3):
for L in itertools.combinations(L_array, 2):
for s0 in s:
loop_array = itertools.permutations(list(L) + list(s) + [s0])
This is probably the most complicated of the $11$ examples. Note the use of itertools.combinations vs itertools.permutations, the latter provides all arrangements and the former does not, which helps us reduce over counting. Over counting is not completely avoided however. The itertools library does not know that our two $\a$ values are repeats so we are over counting by a factor of $2$. This is not ideal, but the storage mechanism used (based on Python sets and dicts) eliminates error duplicate counting, so the only sacrifice is run time.
Considering Operators: $+-\times\div$
We will now take each permutation generated and loop through it's components left to right (i.e. consider the first number, then the first two numbers, then the first three, etc.). For example, given the permutation $100$, $50$, $10$, $2$, $7$, $4$, the first number "generated" is $100$. We then need to check all operations with the first two terms, $100+50$, $100-50$, $100\times 50$, and $100\div 50$ which yields $150$, another hit, but three numbers, $50$, $5000$, and $2$ that are not hits. Those last three numbers are not hits, but cannot be ignored since additional terms may turn them into hits; for example $100\times 50\div 10\div 2=250$ is another hit.
Challenges also arise with the implementation of addition, subtraction, multiplication and division operations in this left-to-right paradigm. We have $5$ spaces in between the $6$ numbers for each operation, for $4^5=1024$ possible permutations of the operators. However, we must only consider those where left to right operation satisfies order of operations. For example, $+$ $-$ $+$ $-$ $-$, $\div$ $\times$ $\div$ $\times$ $\div$, and $\times$ $\div$ $-$ $-$ $+$ are all acceptable but $+$ $\times$ $-$ $-$ $-$ because placing addition before multiplication is the equivalent of adding parentheses. Using the above example, $100+50+10\times2$
Acceptable orders of operation can be found with the following code. This finds all lists of five operators where all multiplication and division occur before all addition and subtraction.
operator_list = [] # Indices for operators, 0,1,2,3 is *,/,+,-
for i4 in xrange(4 ** 5):
cl = [i4 // 256 % 4, i4 // 64 % 4, i4 // 16 % 4, i4 // 4 % 4, i4 % 4]
if good_order(cl):
operator_list.append(cl)
print len(operator_list) # 192
Proving that this covers every possible case is not simple, but it makes intuitive sense that when all permutations of the 6 numbers are considered, the $192$ operators considered are exhaustive.
We now have everything we need to search for every combination. Full implementation can be found here.
A Brief Summary of Results
The combination $5$, $6$, $8$, $9$, $75$, $100$, yields $691$ different possible three-digit numbers, the most for any combination. The combination $1$, $1$, $2$, $2$, $3$, $25$, yields only $20$ possible combinations, the fewest. The top and bottom ten combinations are summarized in the tables below.
| Number | Number of three-digit numbers created |
|---|---|
| $5$, $6$, $8$, $9$, $75$, $100$ | $691$ |
| $5$, $7$, $8$, $9$, $75$, $100$ | $652$ |
| $6$, $7$, $9$, $10$, $75$, $100$ | $650$ |
| $6$, $8$, $9$, $10$, $75$, $100$ | $648$ |
| $3$, $8$, $9$, $10$, $75$, $100$ | $648$ |
| $2$, $5$, $6$, $9$, $75$, $100$ | $643$ |
| $5$, $6$, $8$, $9$, $50$, $100$ | $641$ |
| $5$, $6$, $7$, $9$, $75$, $100$ | $640$ |
| $2$, $5$, $8$, $9$, $75$, $100$ | $638$ |
| $4$, $7$, $9$, $10$, $75$, $100$ | $636$ |
| Number | Number of three-digit numbers created |
|---|---|
| $1$, $1$, $2$, $2$, $3$, $25$ | $20$ |
| $1$, $1$, $2$, $2$, $4$, $25$ | $21$ |
| $1$, $1$, $2$, $3$, $3$, $25$ | $25$ |
| $1$, $1$, $3$, $4$, $4$, $25$ | $34$ |
| $1$, $1$, $2$, $2$, $6$, $25$ | $35$ |
| $1$, $1$, $2$, $2$, $9$, $25$ | $35$ |
| $1$, $1$, $2$, $2$, $5$, $25$ | $35$ |
| $1$, $1$, $2$, $2$, $7$, $25$ | $35$ |
| $1$, $1$, $2$, $2$, $4$, $50$ | $36$ |
| $1$, $1$, $2$, $4$, $4$, $25$ | $36$ |
The table below shows that the best choice to pick two large numbers and four small numbers, but the strategy of picking three large is a close second. An outcome is defined as a three-digit number generated by a particular combination.
| Pattern | Arrangements | Total Outcomes | Average # of Outcomes |
|---|---|---|---|
| $\a\b\c\d\e\mathrm{f}$ | $210$ | $46,663$ | $222.2$ |
| $\Lone\a\a\b\b\c$ | $1440$ | $257,167$ | $178.6$ |
| $\Lone\a\a\b\c\d$ | $3360$ | $865,253$ | $257.5$ |
| $\Lone\a\b\c\d\e$ | $1008$ | $349,921$ | $347.1$ |
| One large | $253.5$ | ||
| $\Lone\Ltwo\a\a\b\b$ | $270$ | $58,221$ | $215.6$ |
| $\Lone\Ltwo\a\a\b\c$ | $2160$ | $694,966$ | $321.7$ |
| $\Lone\Ltwo\a\b\c\d$ | $1260$ | $574,520$ | $456.0$ |
| Two large | $\pmb{359.8}$ | ||
| $\Lone\Ltwo\Lthree\a\a\b$ | $360$ | $100,324$ | $278.7$ |
| $\Lone\Ltwo\Lthree\a\b\c$ | $480$ | $199,349$ | $415.3$ |
| Three large | $356.8$ | ||
| $\Lone\Ltwo\Lthree\Lfour\a\a$ | $10$ | $1,541$ | $154.1$ |
| $\Lone\Ltwo\Lthree\Lfour\a\b$ | $45$ | $10,619$ | $236.0$ |
| Four large | $221.1$ |
The histogram shows what we would intuitively expect, smaller numbers can be computed more often. There are also peaks at multiples of $25$, $50$, and especially $100$, another intuitive byproduct.