Optimal HORSE Strategy
Posted on July 14, 2019
Below is a solution to the Classic problem posed on July 12's edition of the Riddler on fivethirtyeight.com, "What’s The Optimal Way To Play HORSE?".
We will first introduce the game, then walk through a simulation, then the analytic solutions for the simplified game of $\mathrm{H}$ then the full game of $\mathrm{HORSE}$. We'll show that the optimal strategy regardless of the number of letters in the game is to always shoot the highest percentage shot (short of a 100% shot).
Intuitive Strategies
Two strategies immediately come mind. First, take a shot that maximizes the probability of you making a basket and him missing.
The second, and provably better strategy is to take advantage of the one thing you have (you are equally good shooters). You get to go first, so take full advantage of that turn, and maximize the probability of scoring a point before you miss.
Intuitive strategies are meaningless unless testing, so let's see what works best.
Simulation and Optimal Strategy
The code below is a bare bones implementation of a simulation. Player A and Player B can be assigned two different strategies, a_prob and b_prob, and the length of the game can be changed.
import random
def make_basket(prob):
if prob > random.random():
return True
else:
return False
def run_simulation(a_prob, b_prob, horse):
a_score = 0
b_score = 0
a_turn = True
while True:
if a_turn:
if make_basket(a_prob):
if make_basket(a_prob):
pass # both make
else:
a_score += 1 # a make, b miss
else:
a_turn = False # a misses, it's b's turn
else:
if make_basket(b_prob):
if make_basket(b_prob):
pass # both make
else:
b_score += 1 # b make, a miss
else:
a_turn = True # b misses, it's a's turn
if a_score >= horse or b_score >= horse:
break
return a_score, b_score
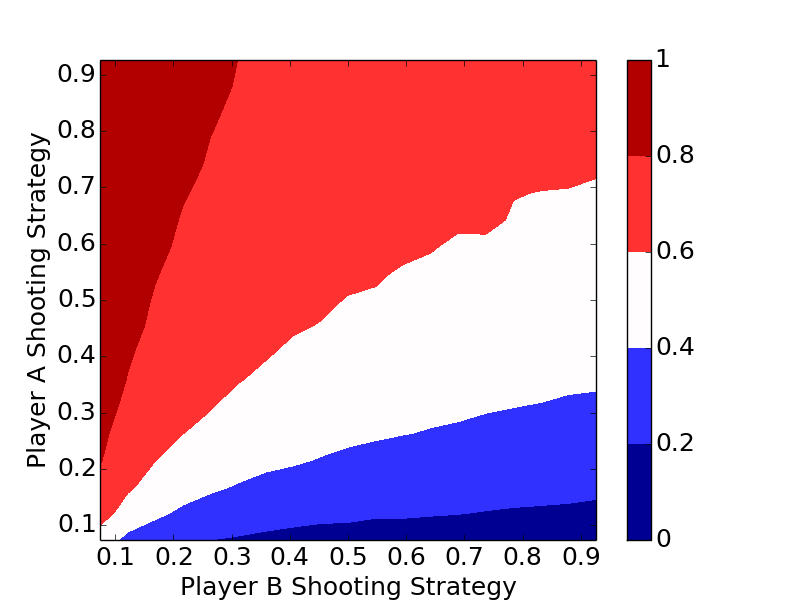
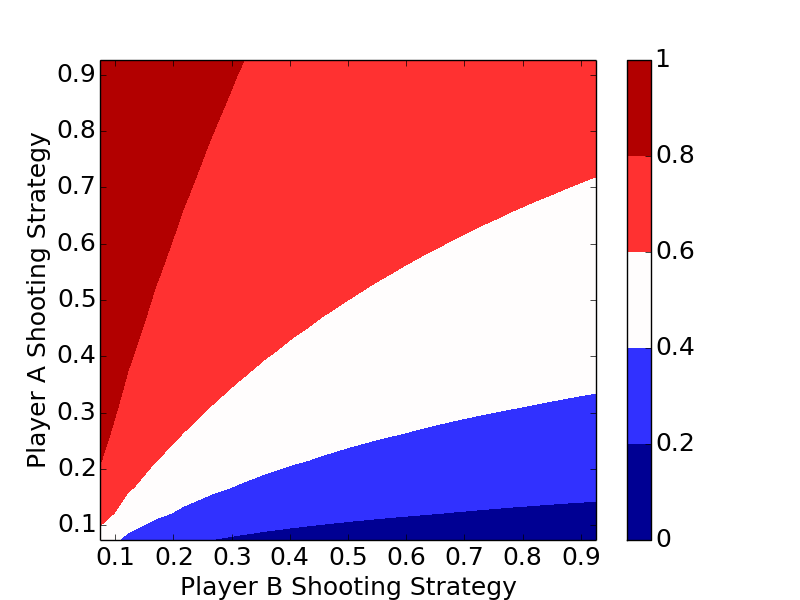
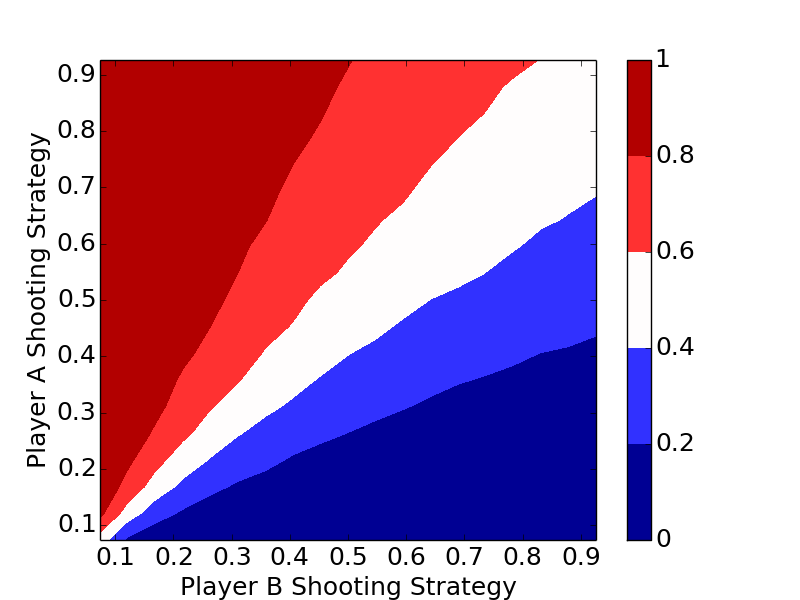
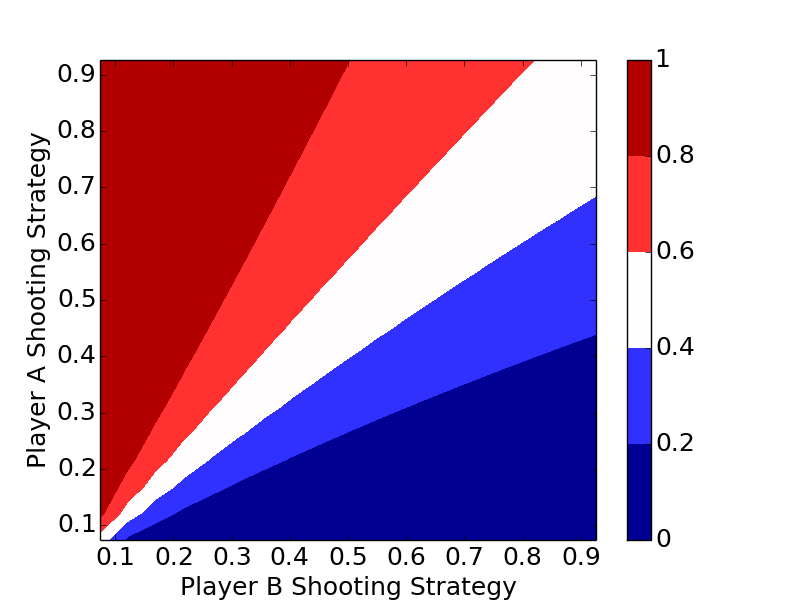
The plots clearly show the optimal strategy regardless of the number of letters in the game is to always shoot the highest percentage shot (short of a 100% shot).
Analytic Solution to $\mathrm{H}$
Let's consider the probability of Player A winning a point before losing their turn. Let $a$ be the probability of Player A making a basket. Then they could make a point in two shots with $p_2(a)=a(1-a)$, in four shots with $p_4(a)=a^3(1-a)$, or in general, in $2n$ shots with $p_{2n}(a)=a^{2n-1}(1-a)$. Therefore, the probability $p_A$ of winning a letter before losing their turn is $$p_A=\sum{p_i(a)}=a(1-a)+a^3(1-a)+... = \frac{a(1-a)}{1-a^2}=\frac{a}{a+1}.$$
The maximum value of this function on $[0,1]$ occurs at $a=1$, with $p_A(a)=0.5$. We wouldn't want to shoot a basket neither player ever misses, a trivial solution and never ending game, but we want to pick the shot closest to that.
We'll expand from winning a point without losing a turn, to winning the game of $H$, another geometric sequence. Let the player's probabilities of winning a point without losing a turn be $p_A$ and $p_B$ respectively. Player A could win on the first turn with probability $p_{AH_{1}}=p_A$, on the third turn with probability $p_{AH_{3}}=(1-p_A)(1-p_B)p_A$, and in $2n+1$ turns with probability $$p_{AH_{ 2n+1}}=(1-p_A)^{n}(1-p_B)^np_A$$
Similarly, the probability that Player A wins $H$, $p_{AH}$, is this sum $$p_{AH}=\sum{p_{AH_{2n+1}}}= \frac{p_A}{1-r}.$$ Where $p_A=\displaystyle\frac{a}{a+1}$, $p_B=\displaystyle\frac{b}{b+1}$, and $r=(1-p_A)(1-p_B)$.
As a sanity check, one could sum the terms of the geometric series for the probability of Player B winning, $\displaystyle\frac{(1-p_A)p_B}{1-r}$, add it to the probability of A winning, and find their sum is one, as it should be.
Analytic Solution to $\mathrm{HORSE}$
Expanding to multi-letter games is no longer a game of compounded geometric series, but instead of counting combinations. You can start by thinking of winning $\mathrm{HORSE}$ the same way as winning a five-game series. Unfortunately, it gets a little more complicated; your probability of winning a letter is based off whether or not you won the previous letter.
Let $A$ denote a Player A point win, and $B$ denote a Player B point win. Consider the game $AAAAA$. On each round, Player A starts, so they have the advantage; their probability of winning each point is $P_{AH}$.
Now consider, $ABAAAA$. The Player A win on point 3 following the Player B win, has the lower likelihood $(1-P_{BH})$ of occurring since Player B had the advantage of starting with the ball after winning point 2.
What makes the counting challenging is that the sequences $AABBBAAA$ and $ABABABAA$, for example, do not have the same probabilities for Player A winning. The first only has two "switches" from who is in control (shooting first), where the second has six switches, changing the probabilities in different ways. There is no way around working through each of the individual $1+5+15+35+70=126$ cases for Player A winning in five through nine games respectively.
The code below summarizes this counting.
probs = [.05*i for i in range(1,20)]
for a in probs:
for b in probs:
pa = a / (1 + a)
pb = b / (1 + b)
r = (1 - pa) * (1 - pb)
pAH = pa / (1 - r) # probability a wins going first
pBH = pb / (1 - r) # probability b wins going first
pAB = (1 - pAH, pAH)
cum_p = 0 # cumulative probability
for s in ['1111', '01111', '001111', '0001111', '00001111']:
tups = list(perm_unique(s))
for tup in tups:
seq = [int(i) for i in list(tup)+['1']]
p = pAB[seq[0]]
for i in range(1, len(seq)):
if seq[i-1] == 0 and seq[i] == 0:
p *= pBH
elif seq[i-1] == 1 and seq[i] == 0:
p *= (1 - pAH)
elif seq[i-1] == 0 and seq[i] == 1:
p *= (1 - pBH)
elif seq[i-1] == 1 and seq[i] == 1:
p *= pAH
cum_p += p
print cum_p,
print ""
My code makes use of some StackOverflow code to make unique permutations.