Counting Sorted Matrix Permutations
Posted on January 13, 2019
Introduction
Consider an $r\times c$ matrix with unique values. It is sorted if each value is greater than the value above it and to its left. E.g. $ \begin{bmatrix} 1& 2 \\ 3 & 4 \end{bmatrix} $ and $ \begin{bmatrix} 1& 3 & 4 \\ 2 & 5 & 6 \end{bmatrix} $ are sorted, but $ \begin{bmatrix} 2& 3 \\ 1 & 4 \end{bmatrix} $ is not since $2>1$.
Our goal is to count the number of unique sorted matrices for a $r \times c$ matrix. WLOG, let the entries of the matrix be the first $n$ natural numbers, where $n=r\cdot c$. One-dimensional matrices have a trivial result; with unique entries, there is a single unique sort. The number of sorted $2\times n$ matrices will be shown to be the $n$th Catalan number, a common sequence in combinatorics.
The five $2\times 3$ (or $3\times 2$, the sorting is symmetric about the transpose) matrices are: $ \begin{bmatrix} 1& 2 & 3 \\ 4 & 5 & 6 \end{bmatrix} $, $ \begin{bmatrix} 1& 2 & 4 \\ 3 & 5 & 6 \end{bmatrix} $, $ \begin{bmatrix} 1& 2 & 5 \\ 3 & 4 & 6 \end{bmatrix} $, $ \begin{bmatrix} 1 & 3 & 4 \\ 2 & 5 & 6 \end{bmatrix} $, and $ \begin{bmatrix} 1& 3 & 5 \\ 2 & 4 & 6 \end{bmatrix} $.
This has long been a problem I wanted to work through. A simple real-life analogy is rooted in a common experience of my own (standing around in formation all day with nothing to do but ponder math problems like this): How many different arrangements of $r\cdot c$ people in a $r\times c$ rectangular formation exist such that each person is taller than the person in front of them and to their left.
Brute Force Counting
A simple algorithm can calculate all sorted permutations, but is computationally costly. The complexity for $n = r\cdot c$ rows and columns is $O(n!)$. The basic pseudo code is
def check_list(test_list, r, c):
for i in xrange(r):
for j in xrange(c):
index = c * i + j
if i > 0 and test_list[index] < test_list[index - c]:
return False
if j > 0 and test_list[index] < test_list[index - 1]:
return False
return True
In this example and all other code examples, $i$ will refer to the row and $j$ to the column. This code brute-force checks an inputted list. It is still the user's responsibility to generate the list, a task with combinatorial run time (and memory usage if implemented poorly). A simple library for generating list permutations in Python is itertools. One would check all $4\times 3$ matrices with the code.
import itertools
r, c=(4, 3)
count = 0
for test_list in itertools.permutations(range(1, r * c + 1)):
if check_list(test_list, r, c):
count += 1
Algorithmic Improvements
One does not want to check all permutations if it can be helped. It is easily observed that, for example, the point in the upper left at $(i, j)=(0, 0)$ must be $v(0, 0)=1$. Furthermore, the bottom right value at $(i, j)=(r-1, c-1)$ must be $v(r-1, c-1)=n$. How do we generalize further?
Consider an arbitrary position $(i,j)$ in the matrix. The value $v(i,j)$ must be greater than every point above and to its left, but inductively also every point to the left of those above it and above those to its left. Basically, every point in the rectangle generated $0$ to $i$ and $0$ to $j$ is less, so the minimum value of $v$ is $v_{\min}(i,j)=(i+1)\cdot(j+1)$.
Similarly, $v$ must be less than every point below and to its right, but inductively also every point to the right of those below it and below those to its right. Therefore the maximum value of $v$ is $v_{\max}(i,j)=r\cdot c-(r-i)\cdot (c-j)+1$.
In the image below, values above and to the left (in blue) must be less than $v$. Values below and to the right must be greater than $v$.
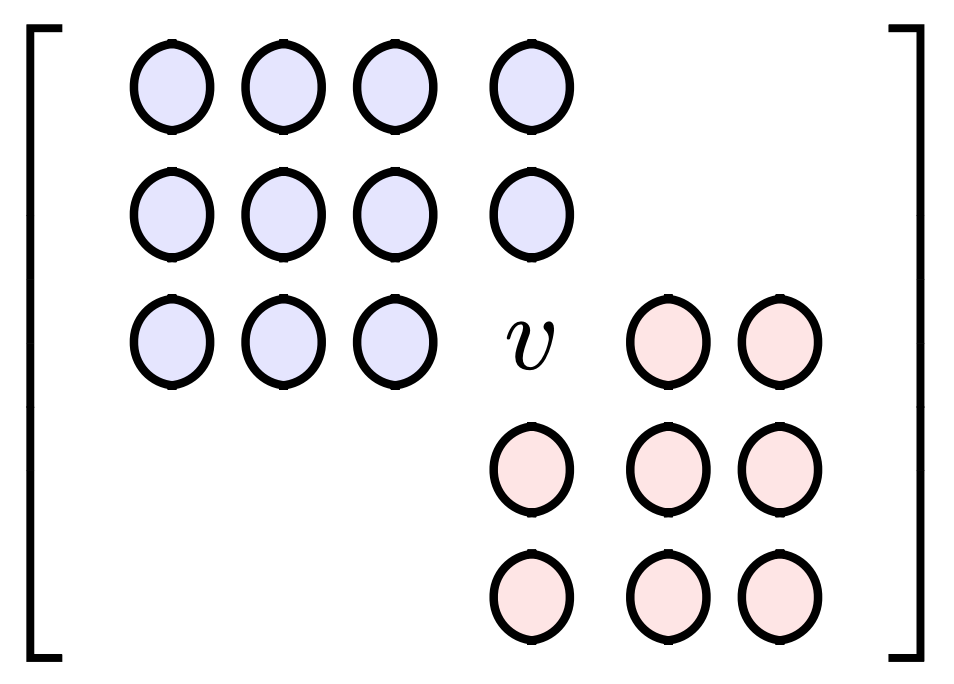
We can improve the bounds further. By the time we get to where $v$ goes, we already have the values to its left and above and those are often more restrictive than the value $(i+1)\cdot (j+1)$. Succinctly, we can improve our lower bound to be $v_{\min}(i,j)=\max\left[ v(i-1,j), v(i,j-1)\right]$.
We can also take advantage of proper data structures to further improve run time. The matrix must have unique values, so as we test values to insert into our list, we need to make sure it's not already in the list. Look-ups in arrays of length $n$ have a run time of $O(n)$. To speed up runtime, we could utilize a Python set in addition to our list, which has roughly $O(1)$ look-up time.
The fully improved code is implemented recursively below.
def recursive_check(test_list, r, c, n, s, count):
if n == r * c:
count += 1
return count
i = n // c # row
j = n % c # col
high = r*c-(r-i)*(c-j)+1
if j == 0:
low = test_list[n - c]
elif i == 0:
low = test_list[n - 1]
else:
low = max(test_list[n - c], test_list[n - 1])
for v in xrange(low, high+1):
if v in s:
continue
test_list.append(v)
s.add(v)
count = recursive_check(test_list, r, c, n + 1, s, count)
test_list.pop(-1)
s.remove(v)
return count
One would check all $4\times 3$ matrices with the code.
r, c=(4, 3)
count = 0
test_list = [1]
s = {1}
count = recursive_check(test_list, r, c, 1, s, count)
Appending and popping from a Python list is typically considered slower than preallocation and assignment, but the array sizes are small enough that the impact is negligible. Python also does it's own pre and reallocation underneath the hood. For more, check out Chapter 3 of High Performance Python.
Note, our code passes a number of variables (six in all) as input to this recursive function, which borders on sloppy. This is not the cleanest approach; one could make the variables global (not recommended), make them attributes of an object and the recursive function a method of that object, or implement a C-structure object (which in Python can be implemented with named tuple or dictionary (see here for more information on implementation). There's always more than one way to skin a cat, just make sure your code is clean.
A comparison of run times is below for a $4\times 3$ matrix in Python. The final algorithm indicates looks ups in a set instead of the original list.
| Algorithm | Run Time |
|---|---|
| Brute Force | 713.0 s |
| Bounded List Look-ups | 0.0128 s |
| Set Look-ups | 0.0101 s |
A comparison of run times is below for a $5\times 4$ matrix in Python.
| Algorithm | Run Time |
|---|---|
| Brute Force | - |
| Bounded List Look-ups | 182.0 s |
| Set Look-ups | 107.3 s |
(Multi-Dimensional) Catalan Numbers
Now that we have a decent algorithm, we can generate a table to summarize the number of sorted matrices.
| r/c | 2 | 3 | 4 | 5 |
|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 |
| 2 | 2 | 5 | 14 | 42 |
| 3 | 5 | 42 | 462 | 6,006 |
| 4 | 14 | 462 | 24,024 | 1,662,804 |
| 5 | 42 | 6,006 | 1,662,804 | 701,149,020 |
| 6 | 132 | 87,516 | 140,229,804 | - |
| 7 | 429 | 1,385,670 | - | - |
| 8 | 1,430 | 23,371,634 | - | - |
| 9 | 4,862 | - | - | - |
As was stated in the Introduction, the 2nd column (and 2nd row) immediately stick out as the Catalan numbers, which show up in all kinds of counting problems. So do the other sequences, like the $3\times n$ or $4\times n$ totals have a home? Integer sequences can be checked against the database at oeis.org. Just enter a comma-separated integer sequence and the site will determine if it's already been discovered. A little more investigation ($3\times n$ search and $4\times n$ search) uncovers the rest of the terms as Higher Dimension Catalan Numbers.
For all this, we merely rediscovered an existing set of sequences (which shouldn't surprise anyone). They have a closed form formula $$ T(m, n) = \frac{0!\cdot 1!\cdot ... \cdot (n-1)! \cdot (m\cdot n)! }{m! \cdot (m+1)! \cdot ...\cdot (m+n-1)! }. $$ Still it was a fun little adventure.